
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点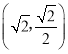 .
.
(1)求椭圆![]() 的方程;
的方程;
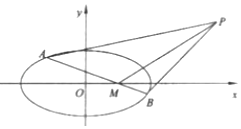
(2)设点![]() ,点
,点![]() 在
在![]() 轴上,过点
轴上,过点![]() 的直线交椭圆
的直线交椭圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
①若直线![]() 的斜率为
的斜率为![]() ,且
,且![]() ,求点
,求点![]() 的坐标;
的坐标;
②设直线![]() ,
,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,是否存在定点
,是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某家具厂有方木料90![]() ,五合板600
,五合板600![]() ,准备加工成书桌和书橱出售.已知生产第张书桌需要方木料O.l
,准备加工成书桌和书橱出售.已知生产第张书桌需要方木料O.l![]() ,五合板2
,五合板2![]() ,生产每个书橱而要方木料0.2
,生产每个书橱而要方木料0.2![]() ,五合板1
,五合板1![]() ,出售一张方桌可获利润80元,出售一个书橱可获利润120元.
,出售一张方桌可获利润80元,出售一个书橱可获利润120元.
(1)如果只安排生产书桌,可获利润多少?
(2)怎样安排生产可使所得利润最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面立角坐标系![]() 中,过点
中,过点![]() 的圆的圆心
的圆的圆心![]() 在
在![]() 轴上,且与过原点倾斜角为
轴上,且与过原点倾斜角为![]() 的直线
的直线![]() 相切.
相切.
(1)求圆![]() 的标准方程;
的标准方程;
(2)点![]() 在直线
在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线
的切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() ,求经过
,求经过![]() 、
、![]() 、
、![]() 、
、![]() 四点的圆所过的定点的坐标.
四点的圆所过的定点的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】某部门在同一上班高峰时段对甲、乙两座地铁站各随机抽取了50名乘客,统计其乘车等待时间(指乘客从进站口到乘上车的时间,乘车等待时间不超过40分钟).将统计数据按![]() ,
,![]() ,
,![]() ,
,![]() 分组,制成频率分布直方图:
分组,制成频率分布直方图:

(1)求![]() 的值;
的值;
(2)记![]() 表示事件“在上班高峰时段某乘客在甲站乘车等待时间少于20分钟”,试估计
表示事件“在上班高峰时段某乘客在甲站乘车等待时间少于20分钟”,试估计![]() 的概率;
的概率;
(3)假设同组中的每个数据用该组区间左端点值来估计,记在上班高峰时段甲、乙两站各抽取的50名乘客乘车的平均等待时间分别为![]() ,
,![]() ,求
,求![]() 的值,并直接写出
的值,并直接写出![]() 与
与![]() 的大小关系.
的大小关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,长半轴长与短半轴长的差为
,长半轴长与短半轴长的差为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若在![]() 轴上存在点
轴上存在点![]() ,过点
,过点![]() 的直线
的直线![]() 分别与椭圆
分别与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() 为定值,求点
为定值,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() 为椭圆
为椭圆![]() 上任意一点,直线
上任意一点,直线![]() 与圆
与圆![]() 交于
交于![]() 两点,点
两点,点![]() 为椭圆
为椭圆![]() 的左焦点.
的左焦点.
(Ⅰ)求椭圆![]() 的离心率及左焦点
的离心率及左焦点![]() 的坐标;
的坐标;
(Ⅱ)求证:直线![]() 与椭圆
与椭圆![]() 相切;
相切;
(Ⅲ)判断![]() 是否为定值,并说明理由.
是否为定值,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】天坛公园是明、清两代皇帝“祭天”“祈谷”的场所.天坛公园中的圜丘台共有三层(如图1所示),上层坛的中心是一块呈圆形的大理石板,从中心向外围以扇面形石(如图2所示).上层坛从第一环至第九环共有九环,中层坛从第十环至第十八环共有九环,下层坛从第十九环至第二十七环共有九环;第一环的扇面形石有9块,从第二环起,每环的扇面形石块数比前一环多9块,则第二十七环的扇面形石块数是______;上、中、下三层坛所有的扇面形石块数是_______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com