
科目: 来源: 题型:
【题目】顺次连接椭圆![]() 的四个顶点恰好构成了一个边长为
的四个顶点恰好构成了一个边长为![]() 且面积为
且面积为![]() 的菱形。
的菱形。
(1)求椭圆![]() 的方程;
的方程;
(2)![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个不同点,若直线
上的两个不同点,若直线![]() ,
,![]() 的斜率之积为
的斜率之积为![]() (以
(以![]() 为坐标原点),线段
为坐标原点),线段![]() 上有一点
上有一点![]() 满足
满足![]() ,连接并延长交椭圆
,连接并延长交椭圆![]() 于点
于点![]() ,求椭圆
,求椭圆![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱锥![]() 中,已知
中,已知![]() 是正三角形,平面
是正三角形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 在棱
在棱![]() 上,且
上,且![]() .
.
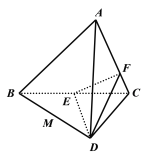
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 的中点,问
的中点,问![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?若存在,说明点
?若存在,说明点![]() 的位置;若不存在,试说明理由.
的位置;若不存在,试说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着“互联网+交通”模式的迅猛发展,“共享助力单车”在很多城市相继出现.某“共享助力单车”运营公司为了解某地区用户对该公司所提供的服务的满意度,随机调查了200名用户,得到用户的满意度评分,现将评分分为5组,如下表:
组别 | 一 | 二 | 三 | 四 | 五 |
满意度评分 |
|
|
|
|
|
频数 | 12 | 28 | 68 |
| 40 |
频率 | 0.06 |
| 0.34 |
| 0.2 |
(1)求表格中的![]() ,
,![]() ,
,![]() 的值;
的值;
(2)估计用户的满意度评分的平均数;
(3)若从这200名用户中随机抽取50人,估计满意度评分高于6分的人数为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】下列四种说法中正确的有______.(填序号)①数据2,2,3,3,4,6,7,3的众数与中位数相等;②数据1,3,5,7,9的方差是数据2,6,10,14,18的方差的一半;③一组数据的方差大小反映该组数据的波动性,若方差越大,则波动性越大,方差越小,则波动性越小.④频率分布直方图中各小长方形的面积等于相应各组的频数.
查看答案和解析>>
科目: 来源: 题型:
【题目】现要完成下列3项抽样调查:①从20罐奶粉中抽取4罐进行食品安全卫生检查;②从某社区100户高收入家庭,270户中等收入家庭,80户低收入家庭中选出45户进行消费水平调查;③某中学报告厅有28排,每排有35个座位,一次报告会恰好坐满了听众,报告会结束后,为了听取意见,需要请28名听众进行座谈.较为合理的抽样方法是( )
A.①系统抽样;②简单随机抽样;③分层抽样
B.①简单随机抽样;②分层抽样;③系统抽样
C.①分层抽样;②系统抽样;③简单随机抽样
D.①简单随机抽样;②系统抽样;③分层抽样
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方体![]() 中,点
中,点![]() 是底面
是底面![]() 的中心,
的中心,![]() 是线段
是线段![]() 的上一点。
的上一点。

(1)若![]() 为
为![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)能否存在点![]() 使得平面
使得平面![]() 平面
平面![]() ,若能,请指出点
,若能,请指出点![]() 的位置关系,并加以证明;若不能,请说明理由。
的位置关系,并加以证明;若不能,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() :
:![]() (
(![]() ,
,![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() :
:![]() .
.
(1)说明![]() 是哪一种曲线,并将
是哪一种曲线,并将![]() 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)若直线![]() 的方程为
的方程为![]() ,设
,设![]() 与
与![]() 的交点为
的交点为![]() ,
,![]() ,
,![]() 与
与![]() 的交点为
的交点为![]() ,
,![]() ,若
,若![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着“北京八分钟”在韩国平昌冬奥会惊艳亮相,冬奥会正式进入了北京周期,全社会对冬奥会的热情空前高涨.
(1)为迎接冬奥会,某社区积极推动冬奥会项目在社区青少年中的普及,并统计了近五年来本社区冬奥项目青少年爱好者的人数![]() (单位:人)与时间
(单位:人)与时间![]() (单位:年),列表如下:
(单位:年),列表如下:

依据表格给出的数据,是否可用线性回归模型拟合![]() 与
与![]() 的关系,请计算相关系数
的关系,请计算相关系数![]() 并加以说明(计算结果精确到0.01).
并加以说明(计算结果精确到0.01).
(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
附:相关系数公式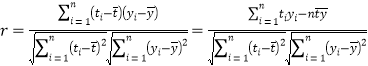 ,参考数据
,参考数据![]() .
.
(2)某冰雪运动用品专营店为吸引广大冰雪爱好者,特推出两种促销方案.
方案一:每满600元可减100元;
方案二:金额超过600元可抽奖三次,每次中奖的概率同为![]() ,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折. v
,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折. v
两位顾客都购买了1050元的产品,并且都选择第二种优惠方案,求至少有一名顾客比选择方案一更优惠的概率;
②如果你打算购买1000元的冰雪运动用品,请从实际付款金额的数学期望的角度分析应该选择哪种优惠方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com