
科目: 来源: 题型:
【题目】高考改革是教育体制改革中的重点领域和关键环节,全社会极其关注.近年来,在新高考改革中,打破文理分科的“![]() ”模式初露端倪.其中“
”模式初露端倪.其中“![]() ”指必考科目语文、数学、外语,“
”指必考科目语文、数学、外语,“![]() ”指考生根据本人兴趣特长和拟报考学校及专业的要求,从物理、化学、生物、历史、政治、地理六科中选择
”指考生根据本人兴趣特长和拟报考学校及专业的要求,从物理、化学、生物、历史、政治、地理六科中选择![]() 门作为选考科目,其中语、数、外三门课各占
门作为选考科目,其中语、数、外三门课各占![]() 分,选考科目成绩采用“赋分制”,即原始分数不直接用,而是按照学生分数在本科目考试的排名来划分等级并以此打分得到最后得分.假定
分,选考科目成绩采用“赋分制”,即原始分数不直接用,而是按照学生分数在本科目考试的排名来划分等级并以此打分得到最后得分.假定![]() 省规定:选考科目按考生成绩从高到低排列,按照占总体
省规定:选考科目按考生成绩从高到低排列,按照占总体![]() 的,以此赋分
的,以此赋分![]() 分、
分、![]() 分、
分、![]() 分、
分、![]() 分.为了让学生们体验“赋分制”计算成绩的方法,
分.为了让学生们体验“赋分制”计算成绩的方法,![]() 省某高中高一(
省某高中高一(![]() )班(共
)班(共![]() 人)举行了以此摸底考试(选考科目全考,单科全班排名,每名学生选三科计算成绩),已知这次摸底考试中的物理成绩(满分
人)举行了以此摸底考试(选考科目全考,单科全班排名,每名学生选三科计算成绩),已知这次摸底考试中的物理成绩(满分![]() 分)频率分布直方图,化学成绩(满分
分)频率分布直方图,化学成绩(满分![]() 分)茎叶图如下图所示,小明同学在这次考试中物理
分)茎叶图如下图所示,小明同学在这次考试中物理![]() 分,化学
分,化学![]() 多分.
多分.

(1)求小明物理成绩的最后得分;
(2)若小明的化学成绩最后得分为![]() 分,求小明的原始成绩的可能值;
分,求小明的原始成绩的可能值;
(3)若小明必选物理,其他两科在剩下的五科中任选,求小明此次考试选考科目包括化学的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() ,定义椭圆
,定义椭圆![]() 上的点
上的点![]() 的“伴随点”为
的“伴随点”为![]() .
.
(1)求椭圆![]() 上的点
上的点![]() 的“伴随点”
的“伴随点”![]() 的轨迹方程;
的轨迹方程;
(2)如果椭圆![]() 上的点
上的点![]() 的“伴随点”为
的“伴随点”为![]() ,对于椭圆
,对于椭圆![]() 上的任意点
上的任意点![]() 及它的“伴随点”
及它的“伴随点”![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)当![]() ,
, ![]() 时,直线
时,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,若点
两点,若点![]() ,
, ![]() 的“伴随点”分别是
的“伴随点”分别是![]() ,
, ![]() ,且以
,且以![]() 为直径的圆经过坐标原点
为直径的圆经过坐标原点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】曲线C是平面内与两个定点![]() ,
,![]() 的距离之积等于常数
的距离之积等于常数![]() 的点的轨迹,给出下列三个结论:
的点的轨迹,给出下列三个结论:
①曲线过坐标原点;②曲线关于坐标原点对称;
③曲线关于横轴对称;④曲线关于纵轴对称;
⑤曲线关于![]() 对称;⑥若点P在曲线上,则
对称;⑥若点P在曲线上,则![]() 的面积不大于
的面积不大于![]() .
.
其中,所有正确结论的序号是______.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 过点
过点![]() 且与直线
且与直线![]() 垂直,直线
垂直,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,动点
轴对称,动点![]() 满足
满足![]() .
.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线
的直线![]() 与轨迹
与轨迹![]() 相交于
相交于![]() 两点,设点
两点,设点![]() ,直线
,直线![]() 的斜率分别为
的斜率分别为![]() ,问
,问![]() 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆![]() 的圆心在直线
的圆心在直线![]() 上,且圆
上,且圆![]() 与
与![]() :
:![]() 相切于点
相切于点![]() .过点
.过点![]() 作两条斜率之积为-2的直线分别交圆
作两条斜率之积为-2的直线分别交圆![]() 于
于![]() ,
,![]() 与
与![]() ,
,![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)设线段![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() ,证明:直线
,证明:直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于点
交于点![]() ,
,![]() 两点.直线
两点.直线![]() ,
,![]() 分别交椭圆
分别交椭圆![]() 于点
于点![]() 、
、![]() (
(![]() ,
,![]() 与
与![]() 不重合)
不重合)
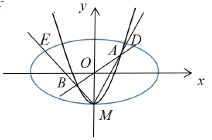
(1)求证:![]() ;
;
(2)若![]() ,求直线
,求直线![]() 的斜率
的斜率![]() 的值;
的值;
(3)若![]() 为坐标原点,直线
为坐标原点,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() ,若
,若![]() ,且
,且![]() ,则
,则![]() 是否为定值?若是,求出定值;若不是,请说明理由.
是否为定值?若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了纪念“一带一路”倡议提出五周年,某城市举办了一场知识竞赛,为了了解市民对“一带一路”知识的掌握情况,从回收的有效答卷中按青年组和老年组各随机抽取了40份答卷,发现成绩都在![]() 内,现将成绩按区间
内,现将成绩按区间![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 进行分组,绘制成如下的频率分布直方图.
进行分组,绘制成如下的频率分布直方图.

青年组

中老年组
(1)利用直方图估计青年组的中位数和老年组的平均数;
(2)从青年组![]() ,
,![]() 的分数段中,按分层抽样的方法随机抽取5份答卷,再从中选出3份答卷对应的市民参加政府组织的座谈会,求选出的3位市民中有2位来自
的分数段中,按分层抽样的方法随机抽取5份答卷,再从中选出3份答卷对应的市民参加政府组织的座谈会,求选出的3位市民中有2位来自![]() 分数段的概率.
分数段的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法正确的个数是( ).
①“若![]() ,则
,则![]() ,
,![]() 中至少有一个不小于2”的逆命题是真命题;
中至少有一个不小于2”的逆命题是真命题;
②命题“设![]() ,若
,若![]() ,则
,则![]() 或
或![]() ”是一个真命题;
”是一个真命题;
③命题![]() ,
,![]() ,则
,则![]() 是
是![]() 的必要不充分条件;
的必要不充分条件;
④命题“![]() ,使得
,使得![]() ”的否定是:“
”的否定是:“![]() ,均有
,均有![]() ”.
”.
A.4B.3C.2D.1
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于点
交于点![]() ,
,![]() 两点.直线
两点.直线![]() ,
,![]() 分别交椭圆
分别交椭圆![]() 于点
于点![]() 、
、![]() (
(![]() ,
,![]() 与
与![]() 不重合)
不重合)
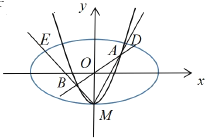
(1)求证:![]() ;
;
(2)若![]() ,求直线
,求直线![]() 的斜率
的斜率![]() 的值;
的值;
(3)若![]() 为坐标原点,直线
为坐标原点,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() ,若
,若![]() ,且
,且![]() ,则
,则![]() 是否为定值?若是,求出定值;若不是,请说明理由.
是否为定值?若是,求出定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com