
科目: 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
![]() 求椭圆的标准方程;
求椭圆的标准方程;
![]() 设直线l经过点
设直线l经过点![]() 且与椭圆C交于不同的两点M,N试问:在x轴上是否存在点Q,使得直线QM与直线QN的斜率的和为定值?若存在,求出点Q的坐标及定值,若不存在,请说明理由.
且与椭圆C交于不同的两点M,N试问:在x轴上是否存在点Q,使得直线QM与直线QN的斜率的和为定值?若存在,求出点Q的坐标及定值,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.

(1)证明:BE⊥DC;
(2)求直线BE与平面PBD所成角的正弦值;
(3)若F为棱PC上一点,满足BF⊥AC,求二面角F-AB-P的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在矩形ABCD中,AB=4,AD=2,E是CD的中点,将△ADE沿AE折起,得到如图2所示的四棱锥D1—ABCE,其中平面D1AE⊥平面ABCE.
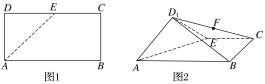
(1)证明:BE⊥平面D1AE;
(2)设F为CD1的中点,在线段AB上是否存在一点M,使得MF∥平面D1AE,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】空气质量按照空气质量指数大小分为七档(五级),相对应空气质量的七个类别,指数越大,说明污染的情况越严重,对人体危害越大.
指数 | 级别 | 类别 | 户外活动建议 |
| Ⅰ | 优 | 可正常活动 |
| Ⅱ | 良 | |
| Ⅲ | 轻微污染 | 易感人群症状有轻度加剧,健康人群出现刺激症状,心脏病和呼吸系统疾病患者应减少体积消耗和户外活动. |
| 轻度污染 | ||
| Ⅳ | 中度污染 | 心脏病和肺病患者症状显著加剧,运动耐受力降低,健康人群中普遍出现症状,老年人和心脏病、肺病患者应减少体力活动. |
| 中度重污染 | ||
| Ⅴ | 重污染 | 健康人运动耐受力降低,由明显强烈症状,提前出现某些疾病,老年人和病人应当留在室内,避免体力消耗,一般人群应尽量减少户外活动. |
现统计邵阳市市区2016年1月至11月连续60天的空气质量指数,制成如图所示的频率分布直方图.
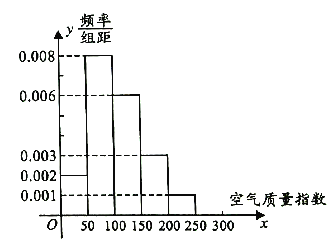
(1)求这60天中属轻度污染的天数;
(2)求这60天空气质量指数的平均值;
(3)一般地,当空气质量为轻度污染或轻度污染以上时才会出现雾霾天气,且此时出现雾霾天气的概率为![]() ,请根据统计数据,求在未来2天里,邵阳市恰有1天出现雾霾天气的概率.
,请根据统计数据,求在未来2天里,邵阳市恰有1天出现雾霾天气的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:对于数列![]() ,如果存在常数
,如果存在常数![]() ,使对任意正整数
,使对任意正整数![]() ,总有
,总有![]() 成立,那么我们称数列
成立,那么我们称数列![]() 为“
为“![]() ﹣摆动数列”.
﹣摆动数列”.
①若![]() ,
,![]() ,
,![]() ,则数列
,则数列![]() _____“
_____“![]() ﹣摆动数列”,
﹣摆动数列”,![]() _____“
_____“![]() ﹣摆动数列”(回答是或不是);
﹣摆动数列”(回答是或不是);
②已知“![]() ﹣摆动数列”
﹣摆动数列”![]() 满足
满足![]() ,
,![]() .则常数
.则常数![]() 的值为_____.
的值为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:
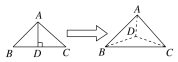
①BD⊥AC;
②△BAC是等边三角形;
③三棱锥D-ABC是正三棱锥;
④平面ADC⊥平面ABC.
其中正确的是( )
A.①②④B.①②③
C.②③④D.①③④
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥![]() 中,底面 ABCD为矩形,侧面为正三角形,且平面
中,底面 ABCD为矩形,侧面为正三角形,且平面![]() 平面
平面 ![]() E 为 PD 中点,AD=2.
E 为 PD 中点,AD=2.
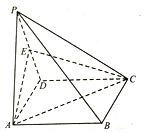
(1)证明平面AEC丄平面PCD;
(2)若二面角![]() 的平面角
的平面角![]() 满足
满足![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名.他发现:“平面内到两个定点![]() ,
,![]() 的距离之比为定值
的距离之比为定值![]() 的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.在平面直角坐标系
的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,点
,点![]() 满足
满足![]() .设点
.设点![]() 的轨迹为
的轨迹为![]() ,下列结论正确的是( )
,下列结论正确的是( )
A.![]() 的方程为
的方程为![]()
B.在![]() 上存在点
上存在点![]() ,使得
,使得![]()
C.当![]() ,
,![]() ,
,![]() 三点不共线时,射线
三点不共线时,射线![]() 是
是![]() 的平分线
的平分线
D.在三棱锥中![]() ,
,![]() 面
面![]() ,且
,且![]() ,
,![]() ,
,![]() ,该三棱锥体积最大值为12
,该三棱锥体积最大值为12
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是某地区2000年至2016年环境基础设施投资额![]() (单位:亿元)的折线图.
(单位:亿元)的折线图.
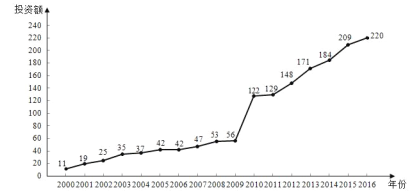
为了预测该地区2018年的环境基础设施投资额,建立了![]() 与时间变量
与时间变量![]() 的两个线性回归模型.根据2000年至2016年的数据(时间变量
的两个线性回归模型.根据2000年至2016年的数据(时间变量![]() 的值依次为1,2,…,17)建立模型
的值依次为1,2,…,17)建立模型
①![]() ;
;
根据2010年至2016年的数据(时间变量![]() 的值依次为1,2,…,7)建立模型
的值依次为1,2,…,7)建立模型
②![]() .
.
利用这两个模型,该地区2018年的环境基础设施投资额的预测值分别为_____,_____;并且可以判断利用模型_____得到的预测值更可靠.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com