【题目】在直角坐标系中，直线的参数方程为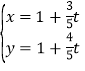（为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为，点的极坐标为.

（1）求的直角坐标方程和的直角坐标；

（2）设与交于，两点，线段的中点为，求.

【题目】已知函数。

（1）若是曲线的切线,求的值；

（2）若,求的取值范围.

新旧个税政策下每月应纳税所得额(含税)计算方法及其对应的税率表如下：

随机抽取某市1000名同一收入层级的从业者的相关资料,经统计分析,预估他们2019年的人均月收入24000元.统计资料还表明,他们均符合住房专项扣除；同时,他们每人至多只有一个符合子女教育扣除的孩子,并且他们之中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是2:1:1:1；此外,他们均不符合其他专项附加扣除.新个税政策下该市的专项附加扣除标准为：住房1000元/月,子女教育每孩1000元/月,赡养老人2000元/月等。

假设该市该收入层级的从业者都独自享受专项附加扣除,将预估的该市该收入层级的从业者的人均月收入视为其个人月收入.根据样本估计总体的思想,解决如下问题：

（1）设该市该收入层级的从业者2019年月缴个税为元,求的分布列和期望；

（2）根据新旧个税方案,估计从2019年1月开始，经过多少个月,该市该收入层级的从业者各月少缴交的个税之和就超过2019年的月收入？

【题目】在平面直角坐标系中,圆外的点在轴的右侧运动,且到圆上的点的最小距离等于它到轴的距离,记的轨迹为.

（1）求的方程；

（2）过点的直线交于,两点,以为直径的圆与平行于轴的直线相切于点,线段交于点,证明：的面积是的面积的四倍.

【题目】已知曲线 y = x3 + x－2 在点 P0 处的切线平行于直线

4x－y－1=0，且点 P0 在第三象限,

⑴求P0的坐标;

⑵若直线, 且 l 也过切点P0 ,求直线l的方程.

【题目】如图,三棱柱中,底面是等边三角形,侧面是矩形,是的中点,是棱上的点,且.

（1）证明：平面；

（2）若,求二面角的余弦值.

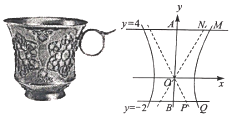
【题目】如图为陕西博物馆收藏的国宝——唐·金筐宝钿团花纹金杯,杯身曲线内收,玲珑娇美,巧夺天工,是唐代金银细作的典范之作.该杯型几何体的主体部分可近似看作是双曲线的右支与直线,,围成的曲边四边形绕轴旋转一周得到的几何体,如图分别为的渐近线与,的交点,曲边五边形绕轴旋转一周得到的几何体的体积可由祖恒原理(祖恒原理：幂势既同，则积不容异).意思是：两等高的几何体在同高处被截得的两截面面积均相等,那么这两个几何体的体积相等，那么这两个几何体的体积相等)，据此求得该金杯的容积是_____.(杯壁厚度忽略不计)

【题目】已知曲线

（1）求曲线在点处的切线方程；

（2）求曲线过点的切线方程

【题目】在平面直角坐标系中,角的顶点为坐标原点,始边与轴的非负半轴重合,终边交单位圆于点,且,则的值是______.

（1）求抛物线E的方程；

（2）不过原点O的动直线l交该抛物线于A，B两点，且满足OA⊥OB，设点Q为圆C上任意一动点，求当动点Q到直线l的距离最大时直线l的方程．