
科目: 来源: 题型:
【题目】“水是生命之源”,但是据科学界统计可用淡水资源仅占地球储水总量的![]() ,全世界近
,全世界近![]() 人口受到水荒的威胁.某市为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准
人口受到水荒的威胁.某市为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨):一位居民的月用水量不超过
(吨):一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.

(1)求直方图中![]() 的值;
的值;
(2)设该市有60万居民,估计全市居民中月均用水量不低于2.5吨的人数,并说明理由;
(3)若该市政府希望使![]() 的居民每月的用水不按议价收费,估计
的居民每月的用水不按议价收费,估计![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,PA=PD![]() ,四边形ABCD为等腰梯形,BC∥AD,BC=CD
,四边形ABCD为等腰梯形,BC∥AD,BC=CD![]() AD=1,E为PA的中点.
AD=1,E为PA的中点.
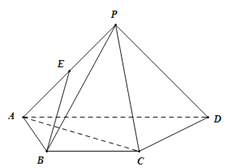
(1)求证:EB∥平面PCD;
(2)求平面PAC与平面PCD所成角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知公差不为0的等差数列{an},其前n项和为Sn,若S10=100,a1,a2,a5成等比数列.
(1)求{an}的通项公式;
(2)bn=anan+1+an+an+1+1,求数列![]() 的前n项和Tn.
的前n项和Tn.
查看答案和解析>>
科目: 来源: 题型:
【题目】2018年9月24日,阿贝尔奖和菲尔兹奖双料得主、英国著名数学家阿蒂亚爵士宣布自己证明了黎曼猜想,这一事件引起了数学界的震动.在1859年,德国数学家黎曼向科学院提交了题目为《论小于某值的素数个数》的论文并提出了一个命题,也就是著名的黎曼猜想.在此之前,著名数学家欧拉也曾研究过这个问题,并得到小于数字![]() 的素数个数大约可以表示为
的素数个数大约可以表示为![]() 的结论.若根据欧拉得出的结论,估计10000以内的素数的个数为(素数即质数,
的结论.若根据欧拉得出的结论,估计10000以内的素数的个数为(素数即质数,![]() ,计算结果取整数)
,计算结果取整数)
A. 1089 B. 1086 C. 434 D. 145
查看答案和解析>>
科目: 来源: 题型:
【题目】F是双曲线![]() 1(a>0,b>0)的左焦点,过点F作双曲线的一条渐近线的垂线,垂足为A,交另一条渐近线于点B.若3
1(a>0,b>0)的左焦点,过点F作双曲线的一条渐近线的垂线,垂足为A,交另一条渐近线于点B.若3![]() ,则此双曲线的离心率为( )
,则此双曲线的离心率为( )
A.2B.3C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4— 4:坐标系与参数方程
设极坐标系与直角坐标系![]() 有相同的长度单位,原点
有相同的长度单位,原点![]() 为极点,
为极点,![]() 轴正半轴为极轴,曲线
轴正半轴为极轴,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 是参数),直线
是参数),直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的参数方程;
的参数方程;
(Ⅱ)设点![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的值﹒
的值﹒
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,直线
,直线![]() :
:![]() .
.
(Ⅰ)设![]() 是
是![]() 图象上一点,
图象上一点,![]() 为原点,直线
为原点,直线![]() 的斜率
的斜率![]() ,若
,若![]() 在
在![]()
![]() 上存在极值,求
上存在极值,求![]() 的取值范围;
的取值范围;
(Ⅱ)是否存在实数![]() ,使得直线
,使得直线![]() 是曲线
是曲线![]() 的切线?若存在,求出
的切线?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(Ⅲ)试确定曲线![]() 与直线
与直线![]() 的交点个数,并说明理由.
的交点个数,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年全国“两会”,即中华人民共和国第十三届全国人大二次会议和中国人民政治协商会议第十三届全国委员会第二次会议,分别于2019年3月5日和3月3日在北京召开.为了了解哪些人更关注“两会”,某机构随机抽取了年龄在15~75岁之间的200人进行调查,并按年龄绘制的频率分布直方图如下图所示,把年龄落在区间[15,35)和[35,75]内的人分别称为“青少年人”和“中老年人”.经统计“青少年人”和“中老年人”的人数之比为19:21.其中“青少年人”中有40人关注“两会”,“中老年人”中关注“两会”和不关注“两会”的人数之比是2:1.
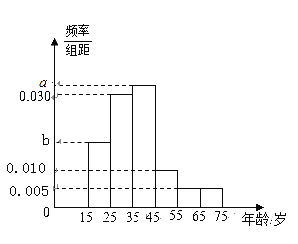
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)现采用分层抽样在[25,35)和[45,55)中随机抽取8名代表,从8人中任选2人,求2人中至少有1个是“中老年人”的概率是多少?
(Ⅲ)根据已知条件,完成下面的2×2列联表,并根据此统计结果判断:能否有99.9%的把握认为“中老年人”比“青少年人”更加关注“两会”?
关注 | 不关注 | 合计 | |
青少年人 | |||
中老年人 | |||
合计 |
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4— 4:坐标系与参数方程
设极坐标系与直角坐标系![]() 有相同的长度单位,原点
有相同的长度单位,原点![]() 为极点,
为极点,![]() 轴正半轴为极轴,曲线
轴正半轴为极轴,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 是参数),直线
是参数),直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的参数方程;
的参数方程;
(Ⅱ)设点![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的值﹒
的值﹒
查看答案和解析>>
科目: 来源: 题型:
【题目】若对满足条件3x+3y+8=2xy(x>0,y>0)的任意x、y,(x+y)2﹣a(x+y)+16≥0恒成立,则实数a的取值范围是( )
A.(﹣∞,8]B.[8,+∞)C.(﹣∞,10]D.[10,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com