
科目: 来源: 题型:
【题目】如果底面是菱形的直棱柱(侧棱与底面垂直的棱柱)![]() 的所有棱长都相等,
的所有棱长都相等,![]() ,E,M,N分别为
,E,M,N分别为![]()
![]()
![]() 的中点,现有下列四个结论:①
的中点,现有下列四个结论:①![]() 平面
平面![]() ②
②![]() ③
③![]() 平面
平面![]() ④异面真线
④异面真线![]() 与MN所成的角的余弦值为
与MN所成的角的余弦值为![]() ,其中正确结论的个数为( )
,其中正确结论的个数为( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标平面内,已知![]() ,其中
,其中![]() 为正整数,对于平面上任意一点
为正整数,对于平面上任意一点![]() ,记
,记![]() 为
为![]() 关于
关于![]() 的对称点,
的对称点,![]() 为
为![]() 关于
关于![]() 的对称点,…
的对称点,…![]() 为
为![]() 关于
关于![]() 的对称点.
的对称点.
(1)求向量![]() 的坐标;
的坐标;
(2)对于任意偶数![]() ,用
,用![]() 表示向量
表示向量![]() 的坐标;
的坐标;
(3)当点![]() 在函数
在函数![]() 图像上移动时,点
图像上移动时,点![]() 形成的是函数
形成的是函数![]() 的图像,其中
的图像,其中![]() 是以3为周期的周期函数,且当
是以3为周期的周期函数,且当![]() 时,
时,![]() ,求:函数
,求:函数![]() 在
在![]() 上的解析式.
上的解析式.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() ,
,![]() 、
、![]() 分别是椭圆短轴的上下两个端点;
分别是椭圆短轴的上下两个端点;![]() 是椭圆的左焦点,P是椭圆上异于点
是椭圆的左焦点,P是椭圆上异于点![]() 、
、![]() 的点,
的点,![]() 是边长为4的等边三角形.
是边长为4的等边三角形.
(1)写出椭圆的标准方程;
(2)设点R满足:![]() ,
,![]() .求证:
.求证:![]() 与
与![]() 的面积之比为定值.
的面积之比为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】高二年级举行一次演讲赛共有10位同学参赛,其中一班有3位,二班有2位,其它班有5位,若采用抽签的方式确定他们的演讲顺序,则一班有3位同学恰好被排在一起(指演讲序号相连),而二班的2位同学没有被排在一起的概率为:( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
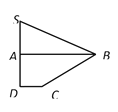
【题目】已知四边形![]() ,点
,点![]() 为线段
为线段![]() 的中点,且
的中点,且![]()
![]() .
. ![]() ,
, ![]() .现将△
.现将△![]() 沿
沿![]() 进行翻折,使得
进行翻折,使得![]()
![]() °,得到图形如图所示,连接
°,得到图形如图所示,连接![]() .
.
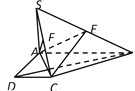
(Ⅰ)若点![]() 在线段
在线段![]() 上,证明:
上,证明: ![]() ;
;
(Ⅱ)若![]() 点为
点为![]() 的中点,求点
的中点,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂用甲、乙两种不同工艺生产一大批同一种零件,零件尺寸均在[21.7,22.3](单位:cm)之间的零件,把零件尺寸在[21.9,22.1)的记为一等品,尺寸在[21.8,21.9)![]() [22.1,22.2)的记为二等品,尺寸在[21.7,21.8)
[22.1,22.2)的记为二等品,尺寸在[21.7,21.8)![]() [22.2,22.3]的记为三等品,现从甲、乙工艺生产的零件中各随机抽取100件产品,所得零件尺寸的频率分布直方图如图所示:
[22.2,22.3]的记为三等品,现从甲、乙工艺生产的零件中各随机抽取100件产品,所得零件尺寸的频率分布直方图如图所示:
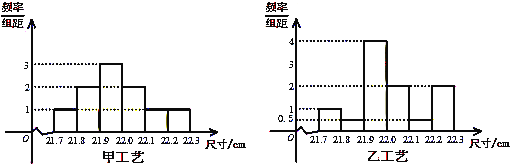
(Ⅰ)根据上述数据完成下列2×2列联表,根据此数据你认为选择不同的工艺与一等品产出率是否有关?
甲工艺 | 乙工艺 | 总计 | |
一等品 | |||
非一等品 | |||
总计 |
P(K2≥k) | 0.1 | 0.05 | 0.01 |
k | 2.706 | 3.841 | 6.635 |
附:![]() ,其中
,其中![]() .
.
(Ⅱ)以上述两种工艺中各种产品的频率作为相应产品产出的概率,若一等品、二等品、三等品的单件利润分别为30元、20元、15元,从一件产品的平均利润考虑,你认为以后该工厂应该选择哪种工艺生产该种零件?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某运动队从![]() 四位运动员中选拔一人参加某项赛事,在选拔结果公布前,甲、乙、丙、丁四位教练对这四位运动员预测如下:甲说:“是
四位运动员中选拔一人参加某项赛事,在选拔结果公布前,甲、乙、丙、丁四位教练对这四位运动员预测如下:甲说:“是![]() 或
或![]() 被选中”; 乙说:“是
被选中”; 乙说:“是![]() 被选中”;丙说:“
被选中”;丙说:“![]() ,
,![]() 均未被选中”; 丁说:“是
均未被选中”; 丁说:“是![]() 被选中”.若这四位教练中只有两位说的话是对的,则获得参赛资格的运动员是____.
被选中”.若这四位教练中只有两位说的话是对的,则获得参赛资格的运动员是____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com