
科目: 来源: 题型:
【题目】如图,在多面体ABD﹣A1B1C1D1中四边形A1B1C1D1,ADD1A1.ABB1A1均为正方形.点M是BD的中点.点H在线段C1M上,且A1H与平面ABD所成角的正弦值为![]() .
.
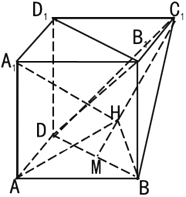
(Ⅰ)证明:B1D1∥平面BC1D:
(Ⅱ)求二面角A﹣A1H﹣B的的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点A(x1,y1),D(x2,y2)其中(x1<x2)是曲线y2=9x(y≥0).上的两点,A,D两点在x轴上的射影分别为点B,C且|BC|=3.
(Ⅰ)当点B的坐标为(1,0)时,求直线AD的方程:
(Ⅱ)记△AOD的面积为S1,梯形ABCD的面积为S2,求![]() 的范围
的范围
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线
为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且设定点
两点,且设定点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面与圆O所在的平面互相垂直.已知AB=2,EF=1.
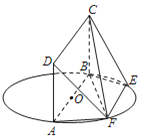
(Ⅰ)求证:平面DAF⊥平面CBF;
(Ⅱ)当AD=1时,求直线FB与平面DFC所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆M过两点A(1,﹣1),B(﹣1,1),且圆心M在x+y﹣2=0上,
(Ⅰ)求圆M的方程;
(Ⅱ)设P是直线x+y+2=0上的动点.PC,PD是圆M的两条切线,C,D为切点,求四边形PCMD面积的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD是边长为1的正方形,MD⊥ABCD,NB⊥ABCD.且MD=NB=1.则下列结论中:
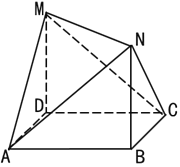
①MC⊥AN
②DB∥平面AMN
③平面CMN⊥平面AMN
④平面DCM∥平面ABN
所有假命题的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.
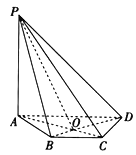
(1)证明:BD⊥PC;
(2)若AD=4,BC=2,设AC∩BD=O,且∠PDO=60°,求四棱锥P-ABCD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com