
科目: 来源: 题型:
【题目】定义函数![]() ,
,![]() (0,
(0,![]() )为
)为![]() 型函数,共中
型函数,共中![]() .
.
(1)若![]() 是
是![]() 型函数,求函数
型函数,求函数![]() 的值域;
的值域;
(2)若![]() 是
是![]() 型函数,求函数
型函数,求函数![]() 极值点个数;
极值点个数;
(3)若![]() 是
是![]() 型函数,在
型函数,在![]() 上有三点A、B、C横坐标分別为
上有三点A、B、C横坐标分別为![]() 、
、![]() 、
、![]() ,其中
,其中![]() <
<![]() <
<![]() ,试判断直线AB的斜率与直线BC的斜率的大小并说明理由.
,试判断直线AB的斜率与直线BC的斜率的大小并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】给定椭圆![]() :
:![]() ,称圆心在原点
,称圆心在原点![]() ,半径为
,半径为![]() 的圆是椭圆
的圆是椭圆![]() 的“准圆”.若椭圆
的“准圆”.若椭圆![]() 的一个焦点为
的一个焦点为![]() ,其短轴上的一个端点到
,其短轴上的一个端点到![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(2)设椭圆短轴的一个端点为![]() ,长轴的一个端点为
,长轴的一个端点为![]() ,点
,点![]() 是“准圆”上一动点,求三角形
是“准圆”上一动点,求三角形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,过点P(0,1)且互相垂直的两条直线分別与圆O:![]() 交于点A,B,与圆M:(x﹣2)2+(y﹣1)2=1交于点C,D.
交于点A,B,与圆M:(x﹣2)2+(y﹣1)2=1交于点C,D.
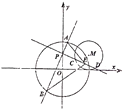
(1)若AB=![]() ,求CD的长;
,求CD的长;
(2)若CD中点为E,求△ABE面积的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某连锁分店销售某种商品,每件商品的成本为4元,并且每件商品需向总店交![]() 元的管理费,预计当每件商品的售价为
元的管理费,预计当每件商品的售价为![]() 元时,一年的销售量为
元时,一年的销售量为![]() 万件.
万件.
(1)求该连锁分店一年的利润![]() (万元)与每件商品的售价
(万元)与每件商品的售价![]() 的函数关系式
的函数关系式![]() ;
;
(2)当每件商品的售价为多少元时,该连锁分店一年的利润![]() 最大,并求出
最大,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】目前用外卖网点餐的人越来越多.现对大众等餐所需时间情况进行随机调查,并将所得数据绘制成频率分布直方图(如图).其中等餐所需时间的范围是![]() ,样本数据分组为
,样本数据分组为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
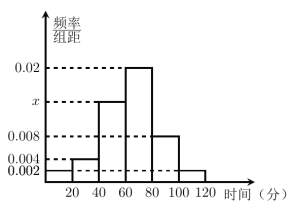
(1)求直方图中![]() 的值;
的值;
(2)某同学在某外卖网点了一份披萨,试估计他等餐时间不多于![]() 小时的概率;
小时的概率;
(3)现有![]() 名学生都分别通过外卖网进行了点餐,这
名学生都分别通过外卖网进行了点餐,这![]() 名学生中等餐所需时间少于
名学生中等餐所需时间少于![]() 小时的人数记为
小时的人数记为![]() ,求
,求![]() 的分布列和数学期望.(以直方图中的频率作为概率)
的分布列和数学期望.(以直方图中的频率作为概率)
查看答案和解析>>
科目: 来源: 题型:
【题目】某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选出了三个科目作为选考科目.若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.某学校为了了解高一年级200名学生选考科目的意向,随机选取20名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有5人 | 5 | 5 | 2 | 1 | 2 | 0 |
选考方案待确定的有7人 | 6 | 4 | 3 | 2 | 4 | 2 | |
女生 | 选考方案确定的有6人 | 3 | 5 | 2 | 3 | 3 | 2 |
选考方案待确定的有2人 | 1 | 2 | 1 | 0 | 1 | 1 |
(1)在选考方案确定的男生中,同时选考物理、化学、生物的人数有多少?
(2)从选考方案确定的男生中任选2名,试求出这2名学生选考科目完全相同的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】邗江中学高二年级某班某小组共10人,利用寒假参加义工活动,已知参加义工活动次数为1,2,3的人数分别为3,3,4.现从这10人中选出2人作为该组代表参加座谈会.
(1)记“选出2人参加义工活动的次数之和为4”为事件![]() ,求事件
,求事件![]() 发生的概率;
发生的概率;
(2)设![]() 为选出2人参加义工活动次数之差的绝对值,求随机变量
为选出2人参加义工活动次数之差的绝对值,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com