
科目: 来源: 题型:
【题目】设![]() 是平面内共始点的三个非零向量,且两两不共线,
是平面内共始点的三个非零向量,且两两不共线,![]() 有下列命题:
有下列命题:
(1)关于![]() 的方程
的方程![]() 可能有两个不同的实数解;
可能有两个不同的实数解;
(2)关于![]() 的方程
的方程![]() 至少有一个实数解;
至少有一个实数解;
(3)关于![]() 的方程
的方程![]() 最多有一个实数解;
最多有一个实数解;
(4)关于![]() 的方程
的方程![]() 若有实数解,则三个向量的终点不可能共线;
若有实数解,则三个向量的终点不可能共线;
上述命题正确的序号是__________
查看答案和解析>>
科目: 来源: 题型:
【题目】将正![]() 分割
分割![]() 成个全等的小正三角形(图1,图2分别给出了
成个全等的小正三角形(图1,图2分别给出了![]() 的情形),在每个三角形的顶点各放置一个数,使位于
的情形),在每个三角形的顶点各放置一个数,使位于![]() 的三边及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列,若顶点
的三边及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列,若顶点![]() 处的三个数互不相同且和为1,记所有顶点上的数的和为
处的三个数互不相同且和为1,记所有顶点上的数的和为![]() ,已知
,已知![]() ,则
,则![]() (用含
(用含![]() 的式子表达)__________
的式子表达)__________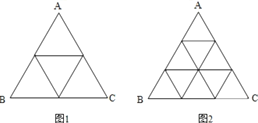
查看答案和解析>>
科目: 来源: 题型:
【题目】椭圆C:![]() 过点M(2,0),且右焦点为F(1,0),过F的直线l与椭圆C相交于A、B两点.设点P(4,3),记PA、PB的斜率分别为k1和k2.
过点M(2,0),且右焦点为F(1,0),过F的直线l与椭圆C相交于A、B两点.设点P(4,3),记PA、PB的斜率分别为k1和k2.
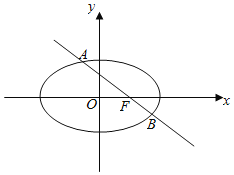
(1)求椭圆C的方程;
(2)如果直线l的斜率等于-1,求出k1k2的值;
(3)探讨k1+k2是否为定值?如果是,求出该定值;如果不是,求出k1+k2的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在下列四个几何体中,它们的三视图(主视图、左视图、俯视图)中有且仅有两个相同,而另一个不同的几何体是( )
(1)棱长为1的正方体

(2)底面直径和高均为1的圆柱

(3)底面直径和高均为1的圆锥

(4)底面边长为1、高为2的正四棱柱

A.(2)(3)(4)B.(1)(2)(3)
C.(1)(3)(4)D.(1)(2)(4)
查看答案和解析>>
科目: 来源: 题型:
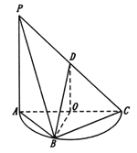
【题目】如图所示,三棱锥![]() 放置在以
放置在以![]() 为直径的半圆面
为直径的半圆面![]() 上,
上,![]() 为圆心,
为圆心,![]() 为圆弧
为圆弧![]() 上的一点,
上的一点,![]() 为线段
为线段![]() 上的一点,且
上的一点,且![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)当二面角![]() 的平面角为
的平面角为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
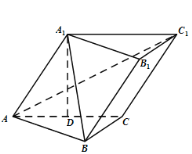
【题目】如图,已知斜三棱柱![]() 中,
中,![]() ,
,![]() 在底面
在底面![]() 上的射影恰为
上的射影恰为![]() 的中点
的中点![]() ,且
,且![]() .
.
(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角![]() 的平面角为
的平面角为![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
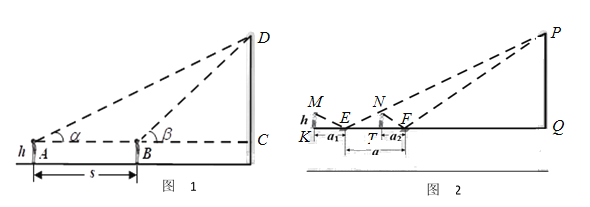
【题目】在数学建模课上,老师给大家带来了一则新闻:“2019年8月16日上午,423米的东莞第一高楼民盈国贸中心2号楼(以下简称“国贸中心”)正式封顶,随着最后一方混凝土浇筑到位,标志着东莞最高楼纪录诞生,由东莞本地航母级企业民盈集团刷新了东莞天际线,比之前的东莞第一高楼台商大厦高出134米.”在同学们的惊叹中,老师提出了问题:国贸中心真有这么高吗?我们能否运用所学知识测量验证一下?一周后,两个兴趣小组分享了他们各自的测量方案.
第一小组采用的是“两次测角法”:他们在国贸中心隔壁的会展中心广场上的![]() 点测得国贸中心顶部的仰角为
点测得国贸中心顶部的仰角为![]() ,正对国贸中心前进了
,正对国贸中心前进了![]() 米后,到达
米后,到达![]() 点,在
点,在![]() 点测得国贸中心顶部的仰角为
点测得国贸中心顶部的仰角为![]() ,然后计算出国贸中心的高度(如图).
,然后计算出国贸中心的高度(如图).
第二小组采用的是“镜面反射法”:在国贸中心后面的新世纪豪园一幢11层楼(与国贸中心处于同一水平面,每层约3米)楼顶天台上,进行两个操作步骤:①将平面镜置于天台地面上,人后退至从镜中能看到国贸大厦的顶部位置,测量出人与镜子的距离为![]() 米;②正对国贸中心,将镜子前移
米;②正对国贸中心,将镜子前移![]() 米,重复①中的操作,测量出人与镜子的距离为
米,重复①中的操作,测量出人与镜子的距离为![]() 米.然后计算出国贸中心的高度(如图).
米.然后计算出国贸中心的高度(如图).
实际操作中,第一小组测得![]() 米,
米,![]() ,
,![]() ,最终算得国贸中心高度为
,最终算得国贸中心高度为![]() ;第二小组测得
;第二小组测得![]() 米,
米,![]() 米,
米,![]() 米,最终算得国贸中心高度为
米,最终算得国贸中心高度为![]() ;假设他们测量者的“眼高
;假设他们测量者的“眼高![]() ”都为
”都为![]() 米.
米.
(1)请你用所学知识帮两个小组完成计算(参考数据:![]() ,
,![]() ,答案保留整数结果);
,答案保留整数结果);
(2)你认为哪个小组的方案更好,说出你的理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂生产![]() 、
、![]() 两种零件,其质量测试按指标划分,指标大于或等于
两种零件,其质量测试按指标划分,指标大于或等于![]() 的为正品,小于
的为正品,小于![]() 的为次品.现随机抽取这两种零件各100个进行检测,检测结果统计如下:
的为次品.现随机抽取这两种零件各100个进行检测,检测结果统计如下:
测试指标 |
|
|
|
|
|
| 8 | 12 | 40 | 30 | 10 |
| 9 | 16 | 40 | 28 | 7 |
(Ⅰ)试分别估计![]() 、
、![]() 两种零件为正品的概率;
两种零件为正品的概率;
(Ⅱ)生产1个零件![]() ,若是正品则盈利50元,若是次品则亏损10元;生产1个零件
,若是正品则盈利50元,若是次品则亏损10元;生产1个零件![]() ,若是正品则盈利60元,若是次品则亏损15元,在(Ⅰ)的条件下:
,若是正品则盈利60元,若是次品则亏损15元,在(Ⅰ)的条件下:
(i)设![]() 为生产1个零件
为生产1个零件![]() 和一个零件
和一个零件![]() 所得的总利润,求
所得的总利润,求![]() 的分布列和数学期望;
的分布列和数学期望;
(ii)求生产5个零件![]() 所得利润不少于160元的概率.
所得利润不少于160元的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】设圆![]() 的圆心为
的圆心为![]() ,直线l过点
,直线l过点![]() 且与x轴不重合,l交圆
且与x轴不重合,l交圆![]() 于
于![]() 两点,过点
两点,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() .
.
(1)证明![]() 为定值,并写出点
为定值,并写出点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,点
两点,点![]() 为椭圆
为椭圆![]() 上一点,若
上一点,若![]() 是以
是以![]() 为底边的等腰三角形,求
为底边的等腰三角形,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com