
科目: 来源: 题型:
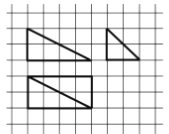
【题目】我国古代数学名著《九章算术·商功》中阐述:“斜解立方,得两壍堵。斜解壍堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以棊,其形露矣.”若称为“阳马”的某几何体的三视图如图所示,图中网格纸上小正方形的边长为1,则对该几何体描述:
①四个侧面都是直角三角形;
②最长的侧棱长为![]() ;
;
③四个侧面中有三个侧面是全等的直角三角形;
④外接球的表面积为![]() .
.
其中正确的个数为( )
A. 0B. 1
C. 2D. 3
查看答案和解析>>
科目: 来源: 题型:
【题目】“科技引领,布局未来”科技研发是企业发展的驱动力量。![]() 年,某企业连续
年,某企业连续![]() 年累计研发投入搭
年累计研发投入搭![]() 亿元,我们将研发投入与经营投入的比值记为研发投入占营收比,这
亿元,我们将研发投入与经营投入的比值记为研发投入占营收比,这![]() 年间的研发投入(单位:十亿元)用右图中的折现图表示,根据折线图和条形图,下列结论错误的使( )
年间的研发投入(单位:十亿元)用右图中的折现图表示,根据折线图和条形图,下列结论错误的使( )
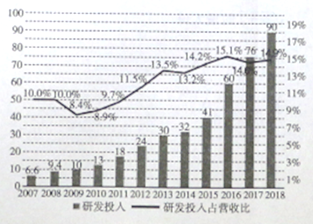
A. ![]() 年至
年至![]() 年研发投入占营收比增量相比
年研发投入占营收比增量相比![]() 年至
年至![]() 年增量大
年增量大
B. ![]() 年至
年至![]() 年研发投入增量相比
年研发投入增量相比![]() 年至
年至![]() 年增量小
年增量小
C. 该企业连续![]() 年研发投入逐年增加
年研发投入逐年增加
D. 该企业来连续![]() 年来研发投入占营收比逐年增加
年来研发投入占营收比逐年增加
查看答案和解析>>
科目: 来源: 题型:
【题目】根据下列条件分别求出直线l的方程.
(1)直线l经过A(4,1),且横、纵截距相等;
(2)直线l平行于直线3x+4y+17=0,并且与两坐标轴围成的三角形的面积为24.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点F是抛物线C:y2=2px(p>0)的焦点,若点P(x0,4)在抛物线C上,且![]() .
.
(1)求抛物线C的方程;
(2)动直线l:x=my+1(m![]() R)与抛物线C相交于A,B两点,问:在x轴上是否存在定点D(t,0)(其中t≠0),使得kAD+kBD=0,(kAD,kBD分别为直线AD,BD的斜率)若存在,求出点D的坐标;若不存在,请说明理由.
R)与抛物线C相交于A,B两点,问:在x轴上是否存在定点D(t,0)(其中t≠0),使得kAD+kBD=0,(kAD,kBD分别为直线AD,BD的斜率)若存在,求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() :
:![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 、
、![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)求线段![]() 的长和
的长和![]() 的积.
的积.
查看答案和解析>>
科目: 来源: 题型:
【题目】槟榔原产于马来西亚,中国主要分布在云南、海南及台湾等热带地区,在亚洲热带地区广泛栽培.槟榔是重要的中药材,在南方一些少数民族还有将果实作为一种咀嚼嗜好品,但其被世界卫生组织国际癌症研究机构列为致癌物清单Ⅰ类致癌物.云南某民族中学为了解![]() ,
,![]() 两个少数民族班学生咀嚼槟榔的情况,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周咀嚼槟榔的颗数作为样本绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
两个少数民族班学生咀嚼槟榔的情况,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周咀嚼槟榔的颗数作为样本绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
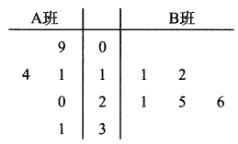
(1)你能否估计哪个班级学生平均每周咀嚼槟榔的颗数较多?
(2)从![]() 班的样本数据中随机抽取一个不超过19的数据记为
班的样本数据中随机抽取一个不超过19的数据记为![]() ,从
,从![]() 班的样本数据中随机抽取一个不超过21的数据记为
班的样本数据中随机抽取一个不超过21的数据记为![]() ,求
,求![]() 的概率;
的概率;
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=x2+2alnx.
(1)若函数f(x)的图象在(2,f(2))处的切线斜率为1,求实数a的值;
(2)若函数![]() 在[1,2]上是减函数,求实数a的取值范围.
在[1,2]上是减函数,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com