
科目: 来源: 题型:
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
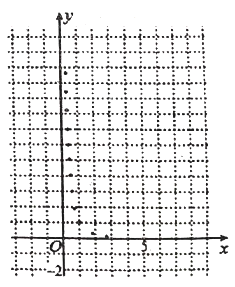
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若单位时间内煤气输出量![]() 与旋转的弧度数
与旋转的弧度数![]() 成正比,那么,利用第(2)问求得的回归方程知
成正比,那么,利用第(2)问求得的回归方程知![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计值分别为
的斜率和截距的最小二乘法估计值分别为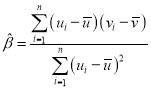 ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知四棱锥PABCD的底面ABCD是矩形,PA⊥底面ABCD,点E、F分别是棱PC、PD的中点,则
①棱AB与PD所在直线垂直;
②平面PBC与平面ABCD垂直;
③△PCD的面积大于△PAB的面积;
④直线AE与直线BF是异面直线.
以上结论正确的是________.(写出所有正确结论的序号)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.

(1) 证明:PB∥平面AEC
(2) 设二面角D-AE-C为60°,AP=1,AD=![]() ,求三棱锥E-ACD的体积
,求三棱锥E-ACD的体积
查看答案和解析>>
科目: 来源: 题型:
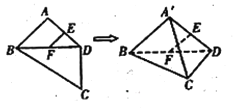
【题目】如图,平面四边形![]() 中,
中,![]() ,
,![]() 是
是![]() ,
,![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,将
,将![]() 沿对角线
沿对角线![]() 折起至
折起至![]() ,使平面
,使平面![]() ,则四面体
,则四面体![]() 中,下列结论不正确的是( )
中,下列结论不正确的是( )
A.![]() 平面
平面![]()
B.异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
C.异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
D.直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】中国剪纸是一种用剪刀或刻刀在纸上剪刻花纹,用于装点生活或配合其他民俗活动的民间艺术;蕴含了极致的数学美和丰富的传统文化信息,现有一幅剪纸的设计图,其中的4个小圆均过正方形的中心,且内切于正方形的两邻边.若在正方形内随机取一点,则该点取自黑色部分的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法中正确的是( )
A.先把高二年级的2000名学生编号:1到2000,再从编号为1到50的学生中随机抽取1名学生,其编号为![]() ,然后抽取编号为
,然后抽取编号为![]() ,
,![]() ,
,![]() ,…的学生,这种抽样方法是分层抽样法
,…的学生,这种抽样方法是分层抽样法
B.线性回归直线![]() 不一定过样本中心
不一定过样本中心![]()
C.若一个回归直线方程为![]() ,则变量
,则变量![]() 每增加一个单位时,
每增加一个单位时,![]() 平均增加3个单位
平均增加3个单位
D.若一组数据2,4,![]() ,8的平均数是5,则该组数据的方差也是5
,8的平均数是5,则该组数据的方差也是5
查看答案和解析>>
科目: 来源: 题型:
【题目】已知两直线方程![]() 与
与![]() ,点
,点![]() 在
在![]() 上运动,点
上运动,点![]() 在
在![]() 上运动,且线段
上运动,且线段![]() 的长为定值
的长为定值![]() .
.
(Ⅰ)求线段![]() 的中点
的中点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)设直线![]() 与点
与点![]() 的轨迹相交于
的轨迹相交于![]() ,
,![]() 两点,
两点,![]() 为坐标原点,若
为坐标原点,若![]() ,求原点
,求原点![]() 的直线
的直线![]() 的距离的取值范围.
的距离的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某水产品经销商销售某种鲜鱼,售价为每千克![]() 元,成本为每千克
元,成本为每千克![]() 元,销售宗旨是当天进货当天销售,如果当天卖不完,那么未售出的部分全部处理,平均每千克损失
元,销售宗旨是当天进货当天销售,如果当天卖不完,那么未售出的部分全部处理,平均每千克损失![]() 元.根据以往的市场调查,将市场日需求量(单位:千克)按
元.根据以往的市场调查,将市场日需求量(单位:千克)按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 进行分组,得到如图的频率分布直方图.
进行分组,得到如图的频率分布直方图.

(Ⅰ)未来连续三天内,连续两天该种鲜钱的日需求量不低于![]() 千克,而另一天的日需求量低于
千克,而另一天的日需求量低于![]() 千克的概率;
千克的概率;
(Ⅱ)在频率分布直方图的日需求量分组中,以各组区间的中点值代表该组的各个值,并以日需求量落入该区间的频率作为日需求量取该区间中点值的概率.若经销商每日进货![]() 千克,记经销商每日利润为
千克,记经销商每日利润为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com