
科目: 来源: 题型:
【题目】如图,已知城市![]() 周边有两个小镇
周边有两个小镇![]() 、
、![]() ,其中乡镇
,其中乡镇![]() 位于城市
位于城市![]() 的正东方
的正东方![]() 处,乡镇
处,乡镇![]() 与城市
与城市![]() 相距
相距![]() ,
,![]() 与
与![]() 夹角的正切值为2,为方便交通,现准备建设一条经过城市
夹角的正切值为2,为方便交通,现准备建设一条经过城市![]() 的公路
的公路![]() ,使乡镇
,使乡镇![]() 和
和![]() 分别位于
分别位于![]() 的两侧,过
的两侧,过![]() 和
和![]() 建设两条垂直
建设两条垂直![]() 的公路
的公路![]() 和
和![]() ,分别与公路
,分别与公路![]() 交汇于
交汇于![]() 、
、![]() 两点,以
两点,以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,建立如图所示的平面直角坐标系
轴,建立如图所示的平面直角坐标系![]() .
.
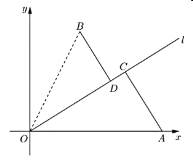
(1)当两个交汇点![]() 、
、![]() 重合,试确定此时
重合,试确定此时![]() 路段长度;
路段长度;
(2)当![]() ,计算此时两个交汇点
,计算此时两个交汇点![]() 、
、![]() 到城市
到城市![]() 的距离之比;
的距离之比;
(3)若要求两个交汇点![]() 、
、![]() 的距离不超过
的距离不超过![]() ,求
,求![]() 正切值的取值范围.
正切值的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】谢尔宾斯基三角形(Sierpinskitriangle)是由波兰数学家谢尔宾斯基在1915年提出的,如图先作一个三角形,挖去一个“中心三角形”(即以原三角形各边的中点为顶点的三角形),然后在剩下的小三角形中又挖去一个“中心三角形”,我们用白色三角形代表挖去的面积,那么灰色三角形为剩下的面积(我们称灰色部分为谢尔宾斯基三角形).若通过该种方法把一个三角形挖3次,然后在原三角形内部随机取一点,则该点取自谢尔宾斯基三角形的概率为______.

查看答案和解析>>
科目: 来源: 题型:
【题目】己知抛物线C:x2=4y的焦点为F,直线l与抛物线C交于A,B两点,延长AF交抛物线C于点D,若AB的中点纵坐标为|AB|-1,则当∠AFB最大时,|AD|=( )
A. 4B. 8C. 16D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在![]() 中,
中,![]() 为直角,
为直角,![]() ,
,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() .
.
(1)试用![]() 、
、![]() 表示向量
表示向量![]() ;
;
(2)在线段![]() 上取一点
上取一点![]() ,在线段
,在线段![]() 上取一点
上取一点![]() ,使得直线
,使得直线![]() 过
过![]() ,设
,设![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,过
,过![]() 作线段
作线段![]() ,使得
,使得![]() 为
为![]() 的中点,且
的中点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是甲、乙、丙三个企业的产品成本(单位:万元)及其构成比例,则下列判断正确的是( )

A. 乙企业支付的工资所占成本的比重在三个企业中最大
B. 由于丙企业生产规模大,所以它的其他费用开支所占成本的比重也最大
C. 甲企业本着勤俭创业的原则,将其他费用支出降到了最低点
D. 乙企业用于工资和其他费用支出额比甲丙都高
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 的内角
的内角![]() 、
、![]() 、
、![]() 的对边分别为
的对边分别为![]() 、
、![]() 、
、![]() ,
,![]() 为
为![]() 内一点,若分别满足下列四个条件:
内一点,若分别满足下列四个条件:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() ;
;
则点![]() 分别为
分别为![]() 的( )
的( )
A.外心、内心、垂心、重心B.内心、外心、垂心、重心
C.垂心、内心、重心、外心D.内心、垂心、外心、重心
查看答案和解析>>
科目: 来源: 题型:
【题目】下列有关平面向量分解定理的四个命题:
(1)一个平面内有且只有一对不平行的向量可作为表示该平面所有向量的基;
(2)一个平面内有无数多对不平行向量可作为表示该平面内所有向量的基;
(3)平面向量的基向量可能互相垂直;
(4)一个平面内任一非零向量都可唯一地表示成该平面内三个互不平行向量的线性组合.
其中正确命题的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】某地统计局就该地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)).
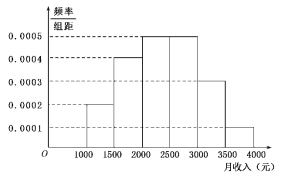
(1)求居民月收入在[2000,2500)的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)在月收入为[2500,3000),[3000,3500),[3500,4000]的三组居民中,采用分层抽样方法抽出90人作进一步分析,则月收入在[3000,3500)的这段应抽多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com