
科目: 来源: 题型:
【题目】甲乙两人玩猜数字游戏,先由甲心中想一个数字,记为![]() ,再由乙猜甲刚才所想的数字,把乙猜的数字记为
,再由乙猜甲刚才所想的数字,把乙猜的数字记为![]() ,其中
,其中![]() ,若
,若![]() ,就称甲乙“心有灵屏”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为( )
,就称甲乙“心有灵屏”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),把曲线
为参数),把曲线![]() 横坐标缩短为原来的
横坐标缩短为原来的![]() ,纵坐标缩短为原来的一半,得到曲线
,纵坐标缩短为原来的一半,得到曲线![]() ,直线
,直线![]() 的普通方程是
的普通方程是![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系;
轴正半轴为极轴建立极坐标系;
(1)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)记射线![]() 与
与![]() 交于点
交于点![]() ,与
,与![]() 交于点
交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,两铁路线垂直相交于站![]() ,若已知
,若已知![]() 千米,甲火车从
千米,甲火车从![]() 站出发,沿
站出发,沿![]() 方向以
方向以![]() 千米
千米![]() 小时的速度行驶,同时乙火车从
小时的速度行驶,同时乙火车从![]() 站出发,沿
站出发,沿![]() 方向,以
方向,以![]() 千米
千米![]() 小时的速度行驶,至
小时的速度行驶,至![]() 站即停止前行(甲车扔继续行驶)(两车的车长忽略不计).
站即停止前行(甲车扔继续行驶)(两车的车长忽略不计).
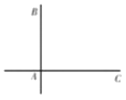
(1)求甲、乙两车的最近距离(用含![]() 的式子表示);
的式子表示);
(2)若甲、乙两车开始行驶到甲,乙两车相距最近时所用时间为![]() 小时,问
小时,问![]() 为何值时
为何值时![]() 最大?
最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() ,
,![]() 是抛物线上的两个动点,且
是抛物线上的两个动点,且![]() ,过
,过![]() ,
,![]() 两点分别作抛物线的切线,设其交点为
两点分别作抛物线的切线,设其交点为![]() .
.
(1)若直线![]() 与
与![]() ,
,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,且
,且![]() 的面积为
的面积为![]() ,求
,求![]() 的值;
的值;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知棱柱![]() 的底面是菱形,且
的底面是菱形,且![]() 面ABCD,
面ABCD,![]() ,F为棱
,F为棱![]() 的中点,M为线段
的中点,M为线段![]() 的中点.
的中点.
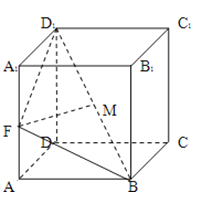
(1)求证:![]() 面ABCD;
面ABCD;
(2)判断直线MF与平面![]() 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(3)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】2018年非洲猪瘟在东北三省出现,为了进行防控,某地生物医药公司派出技术人员对当地一养猪场提供技术服务,收费标准是:每天公司收取养猪场技术服务费120元,当天若需要用药的猪不超过45头,不另外收费,若需要用药的猪超过45头,超过部分每头收取药费8元.
(1)设医药公司日收费为![]() (单位:元),每天需要用药的猪的数量为
(单位:元),每天需要用药的猪的数量为![]() (单位:头),
(单位:头),![]() ,试写出医药公司日收取的费用
,试写出医药公司日收取的费用![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若该医药公司从10月1日起对该养猪场提供技术服务,10月31日该养猪场对其中一个猪舍9月份和10月份猪的发病数量进行了统计,得到如下![]() 列联表.
列联表.
9月份 | 10月份 | 合计 | |
未发病 | 40 | 85 | 125 |
发病 | 65 | 20 | 85 |
合计 | 105 | 105 | 210 |
根据以上列联表,判断是否有99.9%的把握认为猪未发病与医药公司提供技术服务有关?
附:![]() ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】设全集U=R,集合A={x|1≤x<4},B={x|2a≤x<3-a}.
(1)若a=-2,求B∩A,B∩(UA);(2)若A∪B=A,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知不等式|2x-1|+|2x-2|<x+3的解集是A.
(Ⅰ)求集合A;
(Ⅱ)设x,y∈A,对任意a∈R,求证:xy(||x+a|-|y+a||)<x2+y2.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知曲线C1:y=cos x,C2:y=sin (2x+![]() ),则下面结论正确的是( )
),则下面结论正确的是( )
A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com