
科目: 来源: 题型:
【题目】如图,已知直线![]() :
:![]() 和直线
和直线![]() :
:![]() ,射线
,射线![]() 的一个法向量为
的一个法向量为![]() ,点
,点![]() 为坐标原点,且
为坐标原点,且![]() ,直线
,直线![]() 和
和![]() 之间的距离为2,点
之间的距离为2,点![]() ,
,![]() 分别是直线
分别是直线![]() 和
和![]() 上的动点,
上的动点,![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.

(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,
,![]() ,且
,且![]() ,试求
,试求![]() 的最小值;
的最小值;
(3)若![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,如果![]() 与
与![]() 都是整数,就称点
都是整数,就称点![]() 为整点,下列命题中正确的是_____________(写出所有正确命题的编号)
为整点,下列命题中正确的是_____________(写出所有正确命题的编号)
①存在这样的直线,既不与坐标轴平行又不经过任何整点
②如果![]() 与
与![]() 都是无理数,则直线
都是无理数,则直线![]() 不经过任何整点
不经过任何整点
③直线![]() 经过无穷多个整点,当且仅当
经过无穷多个整点,当且仅当![]() 经过两个不同的整点
经过两个不同的整点
④直线![]() 经过无穷多个整点的充分必要条件是:
经过无穷多个整点的充分必要条件是:![]() 与
与![]() 都是有理数
都是有理数
⑤存在恰经过一个整点的直线
查看答案和解析>>
科目: 来源: 题型:
【题目】设椭圆![]()
![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,过
,过![]() 的直线交椭圆于
的直线交椭圆于![]() ,
,![]() 两点,若椭圆
两点,若椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设不经过椭圆的中心而平行于弦![]() 的直线交椭圆
的直线交椭圆![]() 于点
于点![]() ,
,![]() ,设弦
,设弦![]() ,
,![]() 的中点分别为
的中点分别为![]() ,证明:
,证明:![]() 三点共线.
三点共线.
查看答案和解析>>
科目: 来源: 题型:
【题目】2014年7月18日15时,超强台风“威马逊”登陆海南省.据统计,本次台风造成全省直接经济损失119.52亿元.适逢暑假,小明调查住在自己小区的50户居民由于台风造成的经济损失,作出如下频率分布直方图:
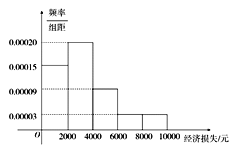
经济损失 4000元以下 | 经济损失 4000元以上 | 合计 | |
捐款超过500元 | 30 | ||
捐款低于500元 | 6 | ||
合计 |
(1)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如上表,在表格空白处填写正确数字,并说明是否有![]() 以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关?
以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关?
(2)台风造成了小区多户居民门窗损坏,若小区所有居民的门窗均由李师傅和张师傅两人进行维修,李师傅每天早上在7:00到8:00之间的任意时刻来到小区,张师傅每天早上在7:30到8:30分之间的任意时刻来到小区,求连续3天内,李师傅比张师傅早到小区的天数的数学期望.
附:临界值表
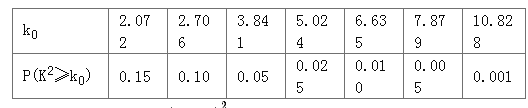
参考公式: ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知甲、乙、丙三位同学在某次考试中总成绩列前三名,有![]() ,
,![]() ,
,![]() 三位学生对其排名猜测如下:
三位学生对其排名猜测如下:![]() :甲第一名,乙第二名;
:甲第一名,乙第二名;![]() :丙第一名;甲第二名;
:丙第一名;甲第二名;![]() :乙第一名,甲第三名.成绩公布后得知,
:乙第一名,甲第三名.成绩公布后得知,![]() ,
,![]() ,
,![]() 三人都恰好猜对了一半,则第一名是__________.
三人都恰好猜对了一半,则第一名是__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列四个命题:
①经过定点![]() 的直线都可以用方程
的直线都可以用方程![]() 表示;
表示;
②经过定点![]() 的直线都可以用方程
的直线都可以用方程![]() 表示;
表示;
③不经过原点的直线都可以用方程![]() 表示;
表示;
④经过任意两个不同的点![]() 、
、![]() 的直线都可以用方程
的直线都可以用方程![]() 表示,
表示,
其中真命题的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() 、
、![]() ,其中,
,其中,![]() ,数列{bn}满足b1=2,bn+1=2bn.
,数列{bn}满足b1=2,bn+1=2bn.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)是否存在自然数![]() ,使得对于任意
,使得对于任意![]() ,
,![]() ,有
,有![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的最小值;
的最小值;
(3)若数列![]() 满足
满足![]()
 ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]()
![]() ,过焦点F的直线l与抛物线交于S,T,且
,过焦点F的直线l与抛物线交于S,T,且![]() .
.

(1)求抛物线C的方程;
(2)设点P是x轴下方(不含x轴)一点,抛物线C上存在不同的两点A,B满足![]()
![]() ,其中
,其中![]() 为常数,且两点D,E均在C上,弦AB的中点为M.
为常数,且两点D,E均在C上,弦AB的中点为M.
①若点P坐标为![]()
![]() ,抛物线过点A,B的切线的交点为N,证明:点N在直线MP上;
,抛物线过点A,B的切线的交点为N,证明:点N在直线MP上;
②若直线PM交抛物线于点Q,求证;![]() 为定值(定值用
为定值(定值用![]() 表示).
表示).
查看答案和解析>>
科目: 来源: 题型:
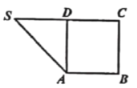
【题目】如图,在直角梯形SABC中,![]() ,D为边SC上的点,且
,D为边SC上的点,且![]() ,现将
,现将![]() 沿AD折起到达
沿AD折起到达![]() 的位置(折起后点S记为P),并使得
的位置(折起后点S记为P),并使得![]() .
.
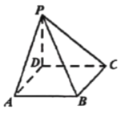
(1)求证:![]() 平面ABCD;
平面ABCD;
(2)设![]() ,
,
①若点E在线段BP上,且满足![]() ,求平面EAC与平面PDC所成的锐二面角的余弦值
,求平面EAC与平面PDC所成的锐二面角的余弦值
②设G是AD的中点,则在![]() 内(含边界)是否存在点F,使得
内(含边界)是否存在点F,使得![]() 平面PBC?若存在,确定点F的位置,若不存在,请说明理由.
平面PBC?若存在,确定点F的位置,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com