
科目: 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,点
的焦点为F,点![]() 在此抛物线上,
在此抛物线上,![]() ,不过原点的直线
,不过原点的直线![]() 与抛物线C交于A,B两点,以AB为直径的圆M过坐标原点.
与抛物线C交于A,B两点,以AB为直径的圆M过坐标原点.
(1)求抛物线C的方程;
(2)证明:直线![]() 恒过定点;
恒过定点;
(3)若线段AB中点的纵坐标为2,求此时直线![]() 和圆M的方程.
和圆M的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】在如图所示的六面体中,四边形![]() 是边长为
是边长为![]() 的正方形,四边形
的正方形,四边形![]() 是梯形,
是梯形,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
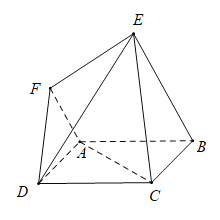
(1)在图中作出平面 ![]() 与平面
与平面![]() 的交线,并写出作图步骤,但不要求证明;
的交线,并写出作图步骤,但不要求证明;
(2)求证:![]() 平面
平面![]() ;
;
(3)求平面![]() 与平面
与平面![]() 所成角的余弦值
所成角的余弦值
查看答案和解析>>
科目: 来源: 题型:
【题目】某手机厂商在销售某型号手机时开展“手机碎屏险”活动.用户购买该型号手机时可选购“手机碎屏险”,保费为![]() 元,若在购机后一年内发生碎屏可免费更换一次屏幕,为了合理确定保费
元,若在购机后一年内发生碎屏可免费更换一次屏幕,为了合理确定保费![]() 的值,该手机厂商进行了问卷调查,统计后得到下表(其中
的值,该手机厂商进行了问卷调查,统计后得到下表(其中![]() 表示保费为
表示保费为![]() 元时愿意购买该“手机碎屏险”的用户比例):
元时愿意购买该“手机碎屏险”的用户比例):

(1)根据上面的数据计算得![]() ,求出
,求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若愿意购买该“手机碎屏险”的用户比例超过![]() ,则手机厂商可以获利,现从表格中的
,则手机厂商可以获利,现从表格中的![]() 种保费任取
种保费任取![]() 种,求这
种,求这![]() 种保费至少有一种能使厂商获利的概率.
种保费至少有一种能使厂商获利的概率.
附:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为 ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=2,AB//DC,AB=2CD,∠BCD=90°.
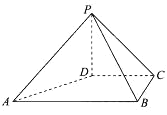
(1)求证:AD⊥PB;
(2)求点C到平面PAB的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】光伏发电是利用太阳能电池及相关设备将太阳光能直接转化为电能.近几年在国内出台的光伏发电补贴政策的引导下,某地光伏发电装机量急剧上涨,如下表:

某位同学分别用两种模型:①![]() ②
②![]() 进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差等于
进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差等于![]() ):
):
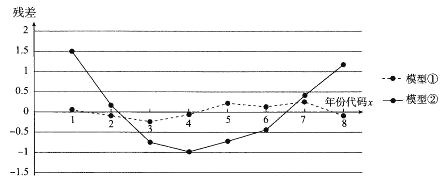
经过计算得![]() ,
,![]() .
.
(1)根据残差图,比较模型①,②的拟合效果,应该选择哪个模型?并简要说明理由.
(2)根据(1)的判断结果及表中数据建立y关于x的回归方程,并预测该地区2020年新增光伏装机量是多少.(在计算回归系数时精确到0.01)
附:归直线的斜率和截距的最小二乘估计公式分别为: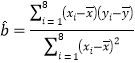 ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】国家统计局统计了我国近10年(2009年2018年)的GDP(GDP是国民经济核算的核心指标,也是衡量一个国家或地区总体经济状况的重要指标)增速的情况,并绘制了下面的折线统计图.

根据该折线统计图,下面说法错误的是
A. 这10年中有3年的GDP增速在9.00%以上
B. 从2010年开始GDP的增速逐年下滑
C. 这10年GDP仍保持6.5%以上的中高速增长
D. 2013年—2018年GDP的增速相对于2009年—2012年,波动性较小
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,且椭圆过点
,且椭圆过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 在
在![]() 上,
上,![]() 是坐标原点,若
是坐标原点,若![]() ,判断四边形
,判断四边形![]() 的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com