
科目: 来源: 题型:
【题目】筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(如图1).因其经济又环保,至今还在农业生产中得到使用(如图2).假定在水流量稳定的情况下,筒车上的每一个盛水筒都做匀速圆周运动.因筒车上盛水筒的运动具有周期性,可以考虑利用三角函数模型刻画盛水筒(视为质点)的运动规律.将筒车抽象为一个几何图形,建立直角坐标系(如图3).设经过t秒后,筒车上的某个盛水筒![]() 从点P0运动到点P.由筒车的工作原理可知,这个盛水筒距离水面的高度H(单位:
从点P0运动到点P.由筒车的工作原理可知,这个盛水筒距离水面的高度H(单位: ![]() ),由以下量所决定:筒车转轮的中心O到水面的距离h,筒车的半径r,筒车转动的角速度ω(单位:
),由以下量所决定:筒车转轮的中心O到水面的距离h,筒车的半径r,筒车转动的角速度ω(单位: ![]() ),盛水筒的初始位置P0以及所经过的时间t(单位:
),盛水筒的初始位置P0以及所经过的时间t(单位:![]() ).已知r=3
).已知r=3![]() ,h=2
,h=2![]() ,筒车每分钟转动(按逆时针方向)1.5圈, 点P0距离水面的高度为3.5
,筒车每分钟转动(按逆时针方向)1.5圈, 点P0距离水面的高度为3.5![]() ,若盛水筒M从点P0开始计算时间,则至少需要经过_______
,若盛水筒M从点P0开始计算时间,则至少需要经过_______![]() 就可到达最高点;若将点
就可到达最高点;若将点![]() 距离水面的高度
距离水面的高度![]() 表示为时间
表示为时间![]() 的函数,则此函数表达式为_________.
的函数,则此函数表达式为_________.



图1 图2 图3
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆![]() 的圆心为
的圆心为![]() ,
,![]() 为圆上任意一点,
为圆上任意一点,![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)记点![]() 的轨迹为曲线
的轨迹为曲线![]() ,点
,点![]() ,
,![]() .若点
.若点![]() 为直线
为直线![]() 上一动点,且
上一动点,且![]() 不在
不在![]() 轴上,直线
轴上,直线![]() 、
、![]() 分别交曲线
分别交曲线![]() 于
于![]() 、
、![]() 两点,求四边形
两点,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,
,![]() 是椭圆
是椭圆![]() 的上顶点,
的上顶点,![]() ,且
,且![]() 的面积为1.
的面积为1.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 、
、![]() 是椭圆
是椭圆![]() 上的两个动点,
上的两个动点,![]() ,求当
,求当![]() 的面积取得最大值时,直线
的面积取得最大值时,直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线![]() 与抛物线
与抛物线![]() 有一个公共点.
有一个公共点.
(1)求抛物线方程;
(2)斜率不为0的直线![]() 经过抛物线
经过抛物线![]() 的焦点
的焦点![]() ,交抛物线于两点
,交抛物线于两点![]() ,
,![]() .抛物线
.抛物线![]() 上是否存在两点
上是否存在两点![]() ,
,![]() 关于直线
关于直线![]() 对称?若存在,求出
对称?若存在,求出![]() 的斜率的取值范围;若不存在,请说明理由.
的斜率的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知2017年![]() 市居民平均家庭净收入走势图(家庭净收入=家庭总收入一家庭总支出),如图所示,则下列说法错误的是( )
市居民平均家庭净收入走势图(家庭净收入=家庭总收入一家庭总支出),如图所示,则下列说法错误的是( )

A. 2017年2月份![]() 市居国民的平均家庭净收入最低
市居国民的平均家庭净收入最低
B. 2017年4,5,6月份![]() 市居民的平均家庭净收入比7、8、9月份的平均家庭净收入波动小
市居民的平均家庭净收入比7、8、9月份的平均家庭净收入波动小
C. 2017年有3个月![]() 市居民的平均家庭净收入低于4000元
市居民的平均家庭净收入低于4000元
D. 2017年9、10、11、12月份平均家庭净收入持续降低
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的左、右焦点分别是
)的左、右焦点分别是![]() ,
,![]() ,点
,点![]() 为
为![]() 的上顶点,点
的上顶点,点![]() 在
在![]() 上,
上,![]() ,且
,且![]() .
.
(1)求![]() 的方程;
的方程;
(2)已知过原点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,垂直于
两点,垂直于![]() 的直线
的直线![]() 过
过![]() 且与椭圆
且与椭圆![]() 交于
交于![]() ,
,![]() 两点,若
两点,若![]() ,求
,求![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,离心率为
,离心率为![]() ,过焦点
,过焦点![]() 且垂直于x轴的直线被椭圆C截得的线段长为1.
且垂直于x轴的直线被椭圆C截得的线段长为1.
![]() Ⅰ
Ⅰ![]() 求椭圆C的方程;
求椭圆C的方程;
![]() Ⅱ
Ⅱ![]() 点
点![]() 为椭圆C上一动点,连接
为椭圆C上一动点,连接![]() ,
,![]() ,设
,设![]() 的角平分线PM交椭圆C的长轴于点
的角平分线PM交椭圆C的长轴于点![]() ,求实数m的取值范围.
,求实数m的取值范围.

查看答案和解析>>
科目: 来源: 题型:
【题目】为了适应新高考改革,某校组织了一次新高考质量测评(总分100分),在成绩统计分析中,抽取12名学生的成绩以茎叶图形式表示如图,学校规定测试成绩低于87分的为“未达标”,分数不低于87分的为“达标”.
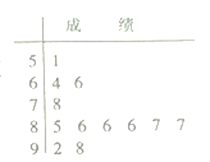
(1)求这组数据的众数和平均数;
(2)在这12名学生中从测试成绩介于80~90之间的学生中任选2人,求至少有1人“达标”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com