【题目】已知点A是椭圆的上顶点，斜率为的直线交椭圆E于A、M两点，点N在椭圆E上，且；

（1）当时，求的面积；

（2）当时，求证：.

【题目】在平行四边形中，，，过点作的垂线，交的延长线于点，.连结，交于点，如图1，将沿折起，使得点到达点的位置，如图2.

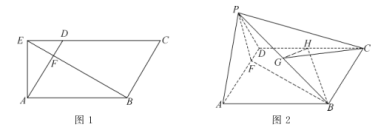
（1）证明：平面平面；

（2）若为的中点，为的中点，且平面平面，求三棱锥的体积.

【题目】2017年5月，来自“一带一路”沿线的20国青年评选出了中国的“新四大发明”：高铁、扫码支付、共享单车和网购.乘坐高铁可以网络购票，为了研究网络购票人群的年龄分布情况，在5月31日重庆到成都高铁9600名网络购票的乘客中随机抽取了120人进行了统计并记录，按年龄段将数据分成6组：，得到如下直方图：

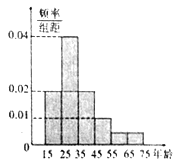
（1）试通过直方图，估计5月31日当天网络购票的9600名乘客年龄的中位数；

（2）若在调查的且年龄在段乘客中随机抽取两人，求两人均来自同一年龄段的概率.

【题目】已知椭圆的离心率为,抛物线的焦点是,是抛物线上的点,H为直线上任一点,A,B分别为椭圆C的上下顶点,且A,B,H三点的连线可以构成三角形.

(Ⅰ)求椭圆C的方程;

(Ⅱ)直线HA,HB与椭圆C的另一交点分别为点D,E,求证:直线DE过定点.

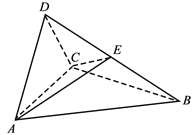
（1）证明：平面ACD⊥平面ABC；

（2）过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D–AE–C的余弦值.

（1）求证：a，b，c成等比数列；

（2）若b＝2，求△ABC的面积的最大值．

【题目】如图，在矩形ABCD中，，E为AB的中点．将沿DE翻折，得到四棱锥．设的中点为M，在翻折过程中，有下列三个命题：

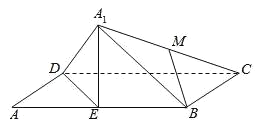
①总有平面；

②线段BM的长为定值；

③存在某个位置，使DE与所成的角为90°．

其中正确的命题是_______．（写出所有正确命题的序号）

【题目】已知集合，且下列三个关系：，，中有且只有一个正确，则函数的值域是__________．

【题目】经观测，某公路段在某时段内的车流量(千辆/小时)与汽车的平均速度(千米/小时)之间有函数关系：．

（1）在该时段内，当汽车的平均速度为多少时车流量最大？最大车流量为多少？(精确到0.01)

（2）为保证在该时段内车流量至少为10千辆/小时，则汽车的平均速度应控制在什么范围内？