
科目: 来源: 题型:
【题目】自贡农科所实地考察,研究发现某贫困村适合种植![]() ,
,![]() 两种药材,可以通过种植这两种药材脱贫.通过大量考察研究得到如下统计数据:药材
两种药材,可以通过种植这两种药材脱贫.通过大量考察研究得到如下统计数据:药材![]() 的亩产量约为300公斤,其收购价格处于上涨趋势,最近五年的价格如下表:
的亩产量约为300公斤,其收购价格处于上涨趋势,最近五年的价格如下表:
编号 | 1 | 2 | 3 | 4 | 5 |
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
单价(元/公斤) | 18 | 20 | 23 | 25 | 29 |
药材![]() 的收购价格始终为20元/公斤,其亩产量的频率分布直方图如下:
的收购价格始终为20元/公斤,其亩产量的频率分布直方图如下:
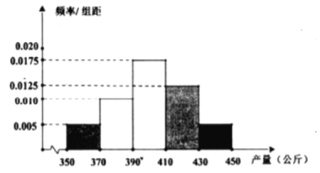
(1)若药材![]() 的单价
的单价![]() (单位:元/公斤)与年份编号
(单位:元/公斤)与年份编号![]() 具有线性相关关系,请求出
具有线性相关关系,请求出![]() 关于
关于![]() 的回归直线方程,并估计2020年药材
的回归直线方程,并估计2020年药材![]() 的单价;
的单价;
(2)用上述频率分布直方图估计药材![]() 的平均亩产量,若不考虑其他因素,试判断2020年该村应种植药材
的平均亩产量,若不考虑其他因素,试判断2020年该村应种植药材![]() 还是药材
还是药材![]() ?并说明理由.
?并说明理由.
参考公式: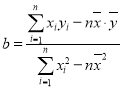 ,
,![]() (回归方程
(回归方程![]() 中)
中)
查看答案和解析>>
科目: 来源: 题型:
【题目】把一个均匀的正方体骰子抛掷两次,观察出现的点数,记第一次出现的点数为![]() ,第二次出现的点数为
,第二次出现的点数为![]() ,设直线
,设直线![]() :
:![]() ,直线
,直线![]() :
:![]() .
.
(1)求直线![]() 和直线
和直线![]() 没有交点的概率;
没有交点的概率;
(2)求直线![]() 和直线
和直线![]() 的交点在第一象限的概率.
的交点在第一象限的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.

(Ⅰ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(Ⅱ)当二面角![]() 的余弦值为
的余弦值为![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成的角.
所成的角.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() ,在圆
,在圆![]() :
:![]() 上任取一点
上任取一点![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .(如图).
.(如图).

(1)求点![]() 的轨迹方程
的轨迹方程![]() ;
;
(2)若过点![]() 的动直线
的动直线![]() 与(1)中的轨迹
与(1)中的轨迹![]() 相交于
相交于![]() 、
、![]() 两点.问:平面内是否存在异于点
两点.问:平面内是否存在异于点![]() 的定点
的定点![]() ,使得
,使得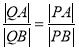 恒成立?试证明你的结论.
恒成立?试证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】某城市交通部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照![]() 分成5组,制成如图所示频率分直方图.
分成5组,制成如图所示频率分直方图.
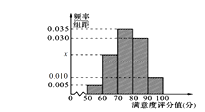
(1)求图中x的值;
(2)求这组数据的平均数和中位数;
(3)已知满意度评分值在![]() 内的男生数与女生数3:2,若在满意度评分值为
内的男生数与女生数3:2,若在满意度评分值为![]() 的人中随机抽取2人进行座谈,求2人均为男生的概率.
的人中随机抽取2人进行座谈,求2人均为男生的概率.
查看答案和解析>>
科目: 来源: 题型:
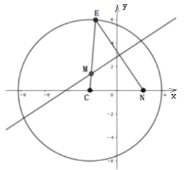
【题目】已知点![]() ,在圆
,在圆![]() :
:![]() 上任取一点
上任取一点![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .(如图).
.(如图).
(1)求点![]() 的轨迹方程
的轨迹方程![]() ;
;
(2)若过点![]() 的动直线
的动直线![]() 与(1)中的轨迹
与(1)中的轨迹![]() 相交于
相交于![]() 、
、![]() 两点.问:平面内是否存在异于点
两点.问:平面内是否存在异于点![]() 的定点
的定点![]() ,使得
,使得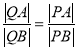 恒成立?试证明你的结论.
恒成立?试证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】椭圆![]() 经过点
经过点![]() ,左、右焦点分别是
,左、右焦点分别是![]() ,
,![]() ,
,![]() 点在椭圆上,且满足
点在椭圆上,且满足![]() 的
的![]() 点只有两个.
点只有两个.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过![]() 且不垂直于坐标轴的直线
且不垂直于坐标轴的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,在
两点,在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 的角平分线是
的角平分线是![]() 轴?若存在求出
轴?若存在求出![]() ,若不存在,说明理由.
,若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某城市交通部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照![]() 分成5组,制成如图所示频率分直方图.
分成5组,制成如图所示频率分直方图.

(1)求图中x的值;
(2)求这组数据的平均数和中位数;
(3)已知满意度评分值在![]() 内的男生数与女生数3:2,若在满意度评分值为
内的男生数与女生数3:2,若在满意度评分值为![]() 的人中随机抽取2人进行座谈,求2人均为男生的概率.
的人中随机抽取2人进行座谈,求2人均为男生的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】等腰直角三角形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() 垂直
垂直![]() 交
交![]() 于
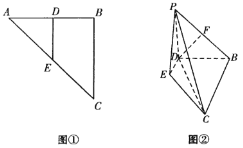
于![]() ,如图①.将
,如图①.将![]() 沿
沿![]() 折起,使
折起,使![]() 到达
到达![]() 的位置,且使平面
的位置,且使平面![]() 平面
平面![]() ,连接
,连接![]() ,
,![]() ,如图②.
,如图②.
(Ⅰ)若![]() 为
为![]() 的中点,
的中点,![]() ,求证:
,求证:![]() ;
;
(Ⅱ)若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com