
科目: 来源: 题型:
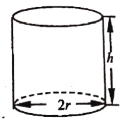
【题目】某企业拟生产一种如图所示的圆柱形易拉罐(上下底面及侧面的厚度不计),易拉罐的体积为![]() ,设圆柱的高度为
,设圆柱的高度为![]() ,底面半径为
,底面半径为![]() ,且
,且![]() ,假设该易拉罐的制造费用仅与其表面积有关.已知易拉罐侧面制造费用为
,假设该易拉罐的制造费用仅与其表面积有关.已知易拉罐侧面制造费用为![]() 元
元![]() ,易拉罐上下底面的制造费用均为
,易拉罐上下底面的制造费用均为![]() 元
元![]() 为常数).
为常数).
(1)写出易拉罐的制造费用![]() (元)关于
(元)关于![]() 的函数表达式,并求其定义域;
的函数表达式,并求其定义域;
(2)求易拉罐制造费用最低时![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某高校在2017年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如表:
组号 | 分组 | 频率 |
第1组 |
|
|
第2组 |
|
|
第3组 |
|
|
第4组 |
|
|
第5组 |
|
|

![]() 求出频率分布表中
求出频率分布表中![]() 处应填写的数据,并完成如图所示的频率分布直方图;
处应填写的数据,并完成如图所示的频率分布直方图;
![]() 根据直方图估计这次自主招生考试笔试成绩的平均数和中位数
根据直方图估计这次自主招生考试笔试成绩的平均数和中位数![]() 结果都保留两位小数
结果都保留两位小数![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了研究学生的数学核心素养与抽象能力(指标![]() )、推理能力(指标
)、推理能力(指标![]() )、建模能力(指标
)、建模能力(指标![]() )的相关性,将它们各自量化为1、2、3三个等级,再用综合指标
)的相关性,将它们各自量化为1、2、3三个等级,再用综合指标![]() 的值评定学生的数学核心素养,若
的值评定学生的数学核心素养,若![]() ,则数学核心素养为一级;若
,则数学核心素养为一级;若![]() ,则数学核心素养为二级;若
,则数学核心素养为二级;若![]() ,则数学核心素养为三级,为了了解某校学生的数学核心素养,调查人员随机访问了某校10名学生,得到如下数据:
,则数学核心素养为三级,为了了解某校学生的数学核心素养,调查人员随机访问了某校10名学生,得到如下数据:
学生编号 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)在这10名学生中任取两人,求这两人的建模能力指标相同条件下综合指标值也相同的概率;
(2)在这10名学生中任取三人,其中数学核心素养等级是一级的学生人数记为![]() ,求随机变量
,求随机变量![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 两点分别在
两点分别在![]() 轴和
轴和![]() 轴上运动,且
轴上运动,且![]() ,若动点
,若动点![]()
满足![]() ,动点
,动点![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)过点![]() 作动直线
作动直线![]() 的平行线交轨迹
的平行线交轨迹![]() 于
于![]() 两点,则
两点,则![]() 是否为定值?若是,求出该值;若不是,说明理由.
是否为定值?若是,求出该值;若不是,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着互联网经济不断发展,网上开店销售农产品的人群越来越多,网上交易额也逐年增加,某一农户农产品连续五年的网银交易额统计表,如下所示:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
网上交易额 | 5 | 6 | 7 | 8 | 10 |
经研究发现,年份与网银交易额之间呈线性相关关系,为了计算的方便,农户将上表的数据进行了处理,![]() ,得到如表:
,得到如表:
时间代号 | 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | 2 | 3 | 5 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)通过(1)中的方程.求出![]() 关于
关于![]() 的回归方程;并用所求回归方程预测到2020年年底,该农户网店网银交易额可达多少?
的回归方程;并用所求回归方程预测到2020年年底,该农户网店网银交易额可达多少?
(附:在线性回归方程![]() 中,
中,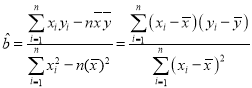 ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆O;x2+y2=4,F1(-1,0),F2(1,0),点D圆O上一动点,2![]() =
=![]() ,点C在直线EF1上,且
,点C在直线EF1上,且![]() =0,记点C的轨迹为曲线W.
=0,记点C的轨迹为曲线W.
(1)求曲线W的方程;
(2)已知N(4,0),过点N作直线l与曲线W交于A,B不同两点,线段AB的中垂线为l',线段AB的中点为Q点,记P与y轴的交点为M,求|MQ|的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com