
科目: 来源: 题型:
【题目】“垛积术”(隙积术)是由北宋科学家沈括在《梦溪笔谈》中首创,南宋数学家杨辉、元代数学家朱世杰丰富和发展的一类数列求和方法,有菱草垛、方垛、刍童垛、三角垛等等,某仓库中部分货物堆放成如图所示的“菱草垛”:自上而下,第一层1件,以后每一层比上一层多1件,最后一层是n件,已知第一层货物单价1万元,从第二层起,货物的单价是上一层单价的![]() .若这堆货物总价是
.若这堆货物总价是![]() 万元,则n的值为( )
万元,则n的值为( )
A. 7B. 8C. 9D. 10
查看答案和解析>>
科目: 来源: 题型:
【题目】某部队在一次军演中要先后执行六项不同的任务,要求是:任务A必须排在前三项执行,且执行任务A之后需立即执行任务E,任务B、任务C不能相邻,则不同的执行方案共有( )
A. 36种B. 44种C. 48种D. 54种
查看答案和解析>>
科目: 来源: 题型:
【题目】对在直角坐标系的第一象限内的任意两点![]() ,
,![]() 作如下定义:
作如下定义:![]() ,那么称点
,那么称点![]() 是点
是点![]() 的“上位点”,同时点
的“上位点”,同时点![]() 是点
是点![]() 的“下位点”.
的“下位点”.
(1)试写出点![]() 的一个“上位点”坐标和一个“下位点”坐标;
的一个“上位点”坐标和一个“下位点”坐标;
(2)设![]() 、
、![]() 、
、![]() 、
、![]() 均为正数,且点
均为正数,且点![]() 是点
是点![]() 的上位点,请判断点
的上位点,请判断点![]() 是否既是点
是否既是点![]() 的“下位点”又是点
的“下位点”又是点![]() 的“上位点”,如果是请证明,如果不是请说明理由;
的“上位点”,如果是请证明,如果不是请说明理由;
(3)设正整数![]() 满足以下条件:对任意实数
满足以下条件:对任意实数![]() ,总存在
,总存在![]() ,使得点
,使得点![]() 既是点
既是点![]() 的“下位点”,又是点
的“下位点”,又是点![]() 的“上位点”,求正整数
的“上位点”,求正整数![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】上饶市在某次高三适应性考试中对数学成绩数据统计显示,全市10000名学生的成绩近似服从正态分布![]() ,现某校随机抽取了50名学生的数学成绩分析,结果这50名学生的成绩全部介于85分到145分之间,现将结果按如下方式分为6组,第一组
,现某校随机抽取了50名学生的数学成绩分析,结果这50名学生的成绩全部介于85分到145分之间,现将结果按如下方式分为6组,第一组![]() ,第二组
,第二组![]() ,…,第六组
,…,第六组![]() ,得到如图所示的频率分布直方图:
,得到如图所示的频率分布直方图:
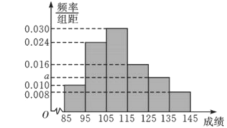
(1)试由样本频率分布直方图估计该校数学成绩的平均分数;
(2)若从这50名学生中成绩在125分(含125分)以上的同学中任意抽取3人,该3人在全市前13名的人数记为![]() ,求
,求![]() 的概率.
的概率.
附:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】下表是某电器销售公司2018年度各类电器营业收入占比和净利润占比统计表:
空调类 | 冰箱类 | 小家电类 | 其它类 | |
营业收入占比 |
|
|
|
|
净利润占比 |
|
|
|
|
则下列判断中不正确的是( )
A. 该公司2018年度冰箱类电器营销亏损
B. 该公司2018年度小家电类电器营业收入和净利润相同
C. 该公司2018年度净利润主要由空调类电器销售提供
D. 剔除冰箱类电器销售数据后,该公司2018年度空调类电器销售净利润占比将会降低
查看答案和解析>>
科目: 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便,工作人员将上表的数据进行了处理, ![]() 得到下表2:
得到下表2:
时间代号t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
(Ⅰ)求z关于t的线性回归方程;
(Ⅱ)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程![]() ,其中
,其中 )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】司机在开机动车时使用手机是违法行为,会存在严重的安全隐患,危及自己和他人的生命. 为了研究司机开车时使用手机的情况,交警部门调查了![]() 名机动车司机,得到以下统计:在
名机动车司机,得到以下统计:在![]() 名男性司机中,开车时使用手机的有
名男性司机中,开车时使用手机的有![]() 人,开车时不使用手机的有
人,开车时不使用手机的有![]() 人;在
人;在![]() 名女性司机中,开车时使用手机的有
名女性司机中,开车时使用手机的有![]() 人,开车时不使用手机的有
人,开车时不使用手机的有![]() 人.
人.
(1)完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为开车时使用手机与司机的性别有关;
的把握认为开车时使用手机与司机的性别有关;
开车时使用手机 | 开车时不使用手机 | 合计 | |
男性司机人数 | |||
女性司机人数 | |||
合计 |
(2)以上述的样本数据来估计总体,现交警部门从道路上行驶的大量机动车中随机抽检3辆,记这3辆车中司机为男性且开车时使用手机的车辆数为![]() ,若每次抽检的结果都相互独立,求
,若每次抽检的结果都相互独立,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
参考公式与数据:
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式
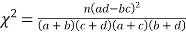 ,其中
,其中![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某教研部门对本地区甲、乙、丙三所学校高三年级进行教学质量抽样调查,甲、乙、丙三所学校高三年级班级数量(单位:个)如下表所示。研究人员用分层抽样的方法从这三所学校中共抽取6个班级进行调查.
学校 | 甲 | 乙 | 丙 |
数量 | 4 | 12 | 8 |
(1)求这6个班级中来自甲、乙、丙三所学校的数量;
(2)若在这6个班级中随机抽取2个班级做进一步调查,
①列举出所有可能的抽取结果;
②求这2个班级来自同一个学校的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某大学毕业生参加一个公司的招聘考试,考试分笔试和面试两个环节,笔试有![]() 、
、![]() 两个题目,该学生答对
两个题目,该学生答对![]() 、
、![]() 两题的概率分别为
两题的概率分别为![]() 、
、![]() ,两题全部答对方可进入面试.面试要回答甲、乙两个问题,该学生答对这两个问题的概率均为
,两题全部答对方可进入面试.面试要回答甲、乙两个问题,该学生答对这两个问题的概率均为![]() ,至少答对一个问题即可被聘用,若只答对一问聘为职员,答对两问聘为助理(假设每个环节的每个题目或问题回答正确与否是相互独立的).
,至少答对一个问题即可被聘用,若只答对一问聘为职员,答对两问聘为助理(假设每个环节的每个题目或问题回答正确与否是相互独立的).
(1)求该学生被公司聘用的概率;
(2)设该学生应聘结束后答对的题目或问题的总个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com