
科目: 来源: 题型:
【题目】已知函数为常数![]()
(1)当![]() 在
在![]() 处取得极值时,若关于x的方程
处取得极值时,若关于x的方程![]() 在
在![]() 上恰有两个不相等的实数根,求实数b的取值范围.
上恰有两个不相等的实数根,求实数b的取值范围.
(2)若对任意的![]() ,总存在
,总存在![]() ,使不等式
,使不等式![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() ,点
,点![]() 与抛物线
与抛物线![]() 的焦点
的焦点![]() 关于原点对称,过点
关于原点对称,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于不同两点
交于不同两点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于两点
交于两点![]() .
.
(Ⅰ)判断是否存在实数![]() 使得四边形
使得四边形![]() 为平行四边形.若存在,求出
为平行四边形.若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(Ⅱ)求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目: 来源: 题型:
【题目】下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
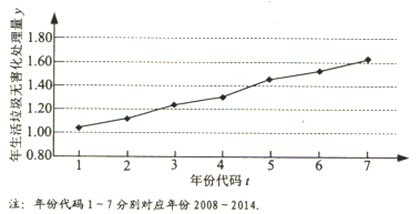
(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据:![]() ,
,![]() ,
,
![]() ,
,![]() ≈2.646.
≈2.646.
参考公式:相关系数
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,
,![]() 是椭圆
是椭圆![]() 的左、右焦点,椭圆
的左、右焦点,椭圆![]() 过点
过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() (不过坐标原点)与椭圆
(不过坐标原点)与椭圆![]() 交于
交于![]() ,
,![]() 两点,且点
两点,且点![]() 在
在![]() 轴上方,点
轴上方,点![]() 在
在![]() 轴下方,若
轴下方,若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目: 来源: 题型:
【题目】“一带一路”沿线的20国青年评选出了中国“新四大发明”:高铁、支付宝、共享单车和网购.2019年春节期间,“支付宝大行动”用发红包的方法刺激支付宝的使用.某商家统计前5名顾客扫描红包所得金额分别为5.2元,2.9元,3.3元,5.9元,4.8元,商家从这5名顾客中随机抽取3人赠送饮水杯.

(1)求获得饮水杯的三人中至少有一人的红包超过5元的概率;
(2)统计一周内每天使用支付宝付款的人数x与商家每天的净利润y元,得到7组数据,如表所示,并作出了散点图.

(i)直接根据散点图判断,![]() 与
与![]() 出哪一个适合作为每天的净利润的回归方程类型.
出哪一个适合作为每天的净利润的回归方程类型.
(ii)根据(i)的判断,建立y关于x的回归方程;若商家当天的净利润至少是1400元,估计使用支付宝付款的人数至少是多少?(a,b,c,d的值取整数)
参考数据:
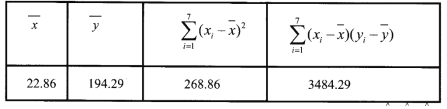
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为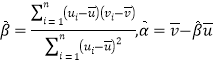 .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】语文中回文句,如:“黄山落叶松叶落山黄,西湖垂柳丝柳垂湖西.”,倒过来读完全一样,数学中也有类似现象,无论从左往右读,还是从右往左读,都是同一个数,称这样的数为“回文数”!二位的回文数有11,22,33,44,55,66,77,88,99,共9个;三位的回文数有101,111,121,131,…,969,979,989,999,共90个;四位的回文数有1001,1111,1221,…,9669,9779,9889,999,共90个;五位的回文数有10001,11111,12221,…,96669,97779,98889,99999共900个,由此推测:10位的回文数总共有_______个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com