
科目: 来源: 题型:
【题目】某新上市的电子产品举行为期一个星期(7天)的促销活动,规定购买该电子产品可免费赠送礼品一份,随着促销活动的有效开展,第五天工作人员对前五天中参加活动的人数进行统计,![]() 表示第
表示第![]() 天参加该活动的人数,得到统计表格如下:
天参加该活动的人数,得到统计表格如下:
| 1 | 2 | 3 | 4 | 5 |
| 4 | 6 | 10 | 23 | 22 |
(1)若![]() 与
与![]() 具有线性相关关系,请根据上表提供的数据,用最小二乘法求出
具有线性相关关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)预测该星期最后一天参加该活动的人数(按四舍五入取到整数).
参考公式: ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在某次测验中,某班40名考生的成绩满分100分统计如图所示.

(Ⅰ)估计这40名学生的测验成绩的中位数![]() 精确到0.1;
精确到0.1;
(Ⅱ)记80分以上为优秀,80分及以下为合格,结合频率分布直方图完成下表,并判断是否有95%的把握认为数学测验成绩与性别有关?
合格 | 优秀 | 合计 | |
男生 | 16 | ||
女生 | 4 | ||
合计 | 40 |
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知曲线![]() 上动点
上动点![]() 与定点
与定点![]() 的距离和它到定直线
的距离和它到定直线![]() 的距离的比是常数
的距离的比是常数![]() .若过
.若过![]() 的动直线
的动直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点.
两点.
(1)判断曲线![]() 的名称并写出它的标准方程;
的名称并写出它的标准方程;
(2)是否存在与点![]() 不同的定点
不同的定点![]() ,使得
,使得![]() 恒成立?若存在,求出点
恒成立?若存在,求出点![]() 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),其中
为参数),其中![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,与
,与![]() 交于
交于![]() 两点,且
两点,且![]() ,求
,求![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】今年入冬以来,我市天气反复.在下图中统计了我市上个月前15天的气温,以及相对去年同期的气温差(今年气温-去年气温,单位:摄氏度),以下判断错误的是( )
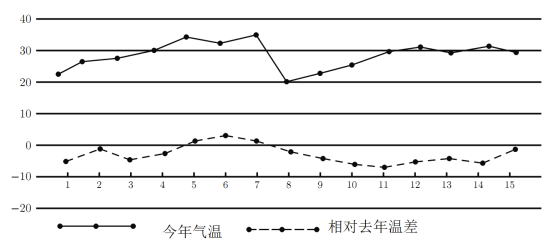
A.今年每天气温都比去年气温低B.今年的气温的平均值比去年低
C.今年8-12号气温持续上升D.今年8号气温最低
查看答案和解析>>
科目: 来源: 题型:
【题目】2018年,依托用户碎片化时间的娱乐需求、分享需求以及视频态的信息负载力,短视频快速崛起;与此同时,移动阅读方兴未艾,从侧面反应了人们对精神富足的一种追求,在习惯了大众娱乐所带来的短暂愉悦后,部分用户依旧对有着传统文学底蕴的严肃阅读青睐有加.
某读书APP抽样调查了非一线城市M和一线城市N各100名用户的日使用时长(单位:分钟),绘制成频率分布直方图如下,其中日使用时长不低于60分钟的用户记为“活跃用户”.
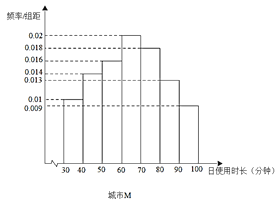
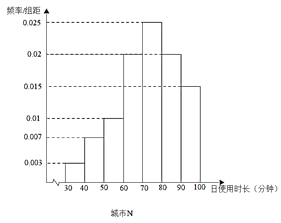
(1)请填写以下![]() 列联表,并判断是否有99.5%的把握认为用户活跃与否与所在城市有关?
列联表,并判断是否有99.5%的把握认为用户活跃与否与所在城市有关?
活跃用户 | 不活跃用户 | 合计 | |
城市M | |||
城市N | |||
合计 |
(2)以频率估计概率,从城市M中任选2名用户,从城市N中任选1名用户,设这3名用户中活跃用户的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
(3)该读书APP还统计了2018年4个季度的用户使用时长y(单位:百万小时),发现y与季度(![]() )线性相关,得到回归直线为
)线性相关,得到回归直线为![]() ,已知这4个季度的用户平均使用时长为12.3百万小时,试以此回归方程估计2019年第一季度(
,已知这4个季度的用户平均使用时长为12.3百万小时,试以此回归方程估计2019年第一季度(![]() )该读书APP用户使用时长约为多少百万小时.
)该读书APP用户使用时长约为多少百万小时.
附:![]() ,其中
,其中![]() .
.
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com