
科目: 来源: 题型:
【题目】已知圆![]() :
:![]() ,动点
,动点![]() ,线段
,线段![]() 与圆
与圆![]() 相交于点
相交于点![]() ,线段
,线段![]() 的长度与点
的长度与点![]() 到
到![]() 轴的距离相等.
轴的距离相等.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,交圆
两点,交圆![]() 于
于![]() ,
,![]() 两点,其中
两点,其中![]() 在线段
在线段![]() 上,
上,![]() 在线段
在线段![]() 上,求
上,求![]() 的最小值及此时直线
的最小值及此时直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为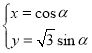 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若点![]() 在曲线
在曲线![]() 上,点
上,点![]() 在曲线
在曲线![]() 上,求
上,求![]() 的最小值及此时点
的最小值及此时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】鲤鱼是中国五千年文化传承的载体之一,它既是拼搏进取、敢于突破自我、敢于冒险奋进精神的载体,又是富裕、吉庆、幸运的美好象征.某水产养殖研究所为发扬传统文化,准备进行“中国红鯉”和“中华彩鲤”杂交育种实验.研究所对200尾中国红鲤和160尾中华彩鲤幼苗进行2个月培育后,将根据体长分别选择生长快的10尾中国红鲤和8尾中华彩鲤作为种鱼进一步培育.为了解培育2个月后全体幼鱼的体长情况,按照品种进行分层抽样,其中共抽取40尾中国红鲤的体长数据(单位:![]() )如下:
)如下:
5 | 6 | 7 | 7.5 | 8 | 8.4 | 4 | 3.5 | 4.5 | 4.3 |
5 | 4 | 3 | 2.5 | 4 | 1.6 | 6 | 6.5 | 5.5 | 5.7 |
3.1 | 5.2 | 4.4 | 5 | 6.4 | 3.5 | 7 | 4 | 3 | 3.4 |
6.9 | 4.8 | 5.6 | 5 | 5.6 | 6.5 | 3 | 6 | 7 | 6.6 |
(1)根据以上样本数据推断,若某尾中国红鲤的体长为![]() ,它能否被选为种鱼?说明理由;
,它能否被选为种鱼?说明理由;
(2)通过计算得到中国红鲤样本数据平均值为![]() ,中华彩鲤样本数据平均值为
,中华彩鲤样本数据平均值为![]() ,求所有样本数据的平均值;
,求所有样本数据的平均值;
(3)如果将8尾中华彩鲤种鱼随机两两组合,求体长最长的2尾组合到一起的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某技术人员在某基地培育了一种植物,一年后,该技术人员从中随机抽取了部分这种植物的高度(单位:厘米)作为样本(样本容量为![]() )进行统计,绘制了如下频率分布直方图,已知抽取的样本植物高度在
)进行统计,绘制了如下频率分布直方图,已知抽取的样本植物高度在![]() 内的植物有8株,在
内的植物有8株,在![]() 内的植物有2株.
内的植物有2株.

(Ⅰ)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() ,
,![]() 的值;
的值;
(Ⅱ)在选取的样本中,从高度在![]() 内的植物中随机抽取3株,设随机变量
内的植物中随机抽取3株,设随机变量![]() 表示所抽取的3株高度在
表示所抽取的3株高度在![]() 内的株数,求随机变量
内的株数,求随机变量![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)据市场调研,高度在![]() 内的该植物最受市场追捧.老王准备前往该基地随机购买该植物50株.现有两种购买方案,方案一:按照该植物的不同高度来付费,其中高度在
内的该植物最受市场追捧.老王准备前往该基地随机购买该植物50株.现有两种购买方案,方案一:按照该植物的不同高度来付费,其中高度在![]() 内的每株10元,其余高度每株5元;方案二:按照该植物的株数来付费,每株6元.请你根据该基地该植物样本的统计分析结果为决策依据,预测老王采取哪种付费方式更便宜?
内的每株10元,其余高度每株5元;方案二:按照该植物的株数来付费,每株6元.请你根据该基地该植物样本的统计分析结果为决策依据,预测老王采取哪种付费方式更便宜?
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校为调查高二年级学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1))和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高(单位:![]() )在
)在![]() 内的男生人数有16人.
内的男生人数有16人.
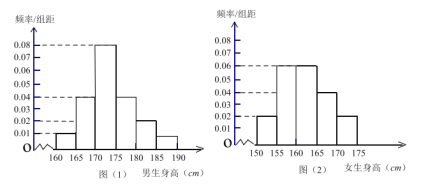
(Ⅰ)求在抽取的学生中,男女生各有多少人?
(Ⅱ)根据频率分布直方图,完成下列的![]() 列联表,并判断能有多大(百分之几)的把握认为“身高与性别有关”?
列联表,并判断能有多大(百分之几)的把握认为“身高与性别有关”?
|
| 总计 | |
男生人数 | |||
女生人数 | |||
总计 |
附:参考公式和临界值表:
 ,
,
| 5.024 | 6.635 | 7.879 | 10.828 |
| 0.025 | 0.010 | 0.005 | 0.001 |
查看答案和解析>>
科目: 来源: 题型:
【题目】某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
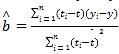 ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】中国古代儒家提出的“六艺”指:礼乐射御书数.某校国学社团预在周六开展“六艺”课程讲座活动,周六这天准备排课六节,每艺一节,排课有如下要求:“乐”与“书”不能相邻,“射”和“御”要相邻,则针对“六艺”课程讲座活动的不同排课顺序共有( )
A.18种B.36种C.72种D.144种
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在圆柱![]() 中,点
中,点![]() 、
、![]() 分别为上、下底面的圆心,平面
分别为上、下底面的圆心,平面![]() 是轴截面,点
是轴截面,点![]() 在上底面圆周上(异于
在上底面圆周上(异于![]() 、
、![]() ),点
),点![]() 为下底面圆弧
为下底面圆弧![]() 的中点,点
的中点,点![]() 与点
与点![]() 在平面
在平面![]() 的同侧,圆柱
的同侧,圆柱![]() 的底面半径为1,高为2.
的底面半径为1,高为2.
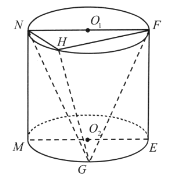
(1)若平面![]() 平面
平面![]() ,证明:
,证明:![]() ;
;
(2)若直线![]() 平面
平面![]() ,求
,求![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知平面直角坐标系![]() ,直线
,直线![]() 过点
过点![]() ,且倾斜角为
,且倾斜角为![]() ,以
,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的参数方程和圆
的参数方程和圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的倾斜角的
的倾斜角的![]() 值.
值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,除
的包裹,除![]() 收费
收费![]() 元之外,超过
元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.该公司将最近承揽的
元.该公司将最近承揽的![]() 件包裹的重量统计如下:
件包裹的重量统计如下:
包裹重量(单位: |
|
|
|
|
|
包裹件数 |
|
|
|
|
|
公司对近![]() 天,每天揽件数量统计如下表:
天,每天揽件数量统计如下表:
包裹件数范围 |
|
|
|
|
|
包裹件数 (近似处理) |
|
|
|
|
|
天数 |
|
|
|
|
|
以上数据已做近似处理,并将频率视为概率.
(1)计算该公司未来![]() 天内恰有
天内恰有![]() 天揽件数在
天揽件数在![]() 之间的概率;
之间的概率;
(2)(i)估计该公司对每件包裹收取的快递费的平均值;
(ii)公司将快递费的三分之一作为前台工作人员的工资和公司利润,剩余的用作其他费用.目前前台有工作人员![]() 人,每人每天揽件不超过
人,每人每天揽件不超过![]() 件,工资
件,工资![]() 元.公司正在考虑是否将前台工作人员裁减
元.公司正在考虑是否将前台工作人员裁减![]() 人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润更有利?
人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润更有利?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com