
科目: 来源: 题型:
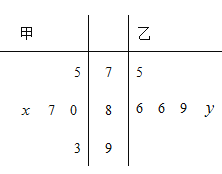
【题目】在学校组织的英语单词背诵比赛中,5位评委对甲、乙两名同学的评分如茎叶图所示(分数为整数,且满分100分),若甲同学所得评分的中位数为87,乙同学所得评分的唯一众数为86,则甲同学所得评分的平均数不小于乙同学所得评分的平均数的概率为______.
查看答案和解析>>
科目: 来源: 题型:
【题目】每年圣诞节,各地的餐馆都出现了用餐需预定的现象,致使--些人在没有预定的情况下难以找到用餐的餐馆,针对这种现象,专家对人们“用餐地点"以及“性别”作出调查,得到的情况如下表所示:
在家用餐 | 在餐馆用餐 | 总计 | |
女性 |
| ||
男性 |
| ||
总计 |
|
|
(1)完成上述![]() 列联表;
列联表;
(2)根据表中的数据,试通过计算判断是否有![]() 的把握说明“用餐地点”与“性别"有关;
的把握说明“用餐地点”与“性别"有关;
(3)若在接受调查的所有人男性中按照“用餐地点”进行分层抽样,随机抽取![]() 人,再在
人,再在![]() 人中抽取
人中抽取![]() 人赠送餐馆用餐券,记收到餐馆用餐券的男性中在餐馆用餐的人数为
人赠送餐馆用餐券,记收到餐馆用餐券的男性中在餐馆用餐的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
|
|
|
|
|
|
|
|
![]()
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】袋子中有四个小球,分别写有“美、丽、华、一”四个字,有放回地从中任取一个小球,直到“华”“一”两个字都取到就停止,用随机模拟的方法估计恰好在第四次停止的概率.利用计算机随机产生0到3之间取整数值的随机数,分别用0,1,2,3代表“美、丽、华、一”这四个字,以每四个随机数为一组,表示取球四次的结果,经随机模拟产生了以下20组随机数:
2323 3211 2303 1233 0211 1322 2201 2213 0012 1231
2312 1300 2331 0312 1223 1031 3020 3223 3301 3212
由此可以估计,恰好第四次就停止的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种,若普通![]() 座以下私家车投保交强险第一年的费用(基准保费)统一为
座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
交强险浮动因素和浮动费率比率表 | ||
浮动因素 | 浮动比率 | |
| 上一年度未发生有责任道路交通事故 | 下浮 |
| 上两年度未发生有责任道路交通事故 | 下浮 |
| 上三年度未发生有责任道路交通事故 | 下浮 |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 |
|
| 上一个年度发生两次及两次以上有责任不涉及死亡的道路交通事故 | 上浮 |
| 上一个年度发生有责任交通死亡事故 | 上浮 |
某机构为了解某一品牌普通![]() 座以下私家车的投保情况,随机抽取了
座以下私家车的投保情况,随机抽取了![]() 辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
|
数量 |
|
|
|
|
|
以这![]() 辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定,![]() ,记
,记![]() 为某同学家的一辆该品牌车在第四年续保时的费用,求
为某同学家的一辆该品牌车在第四年续保时的费用,求![]() 的分布列与数学期望;(数学期望值保留到个位数字)
的分布列与数学期望;(数学期望值保留到个位数字)
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车,假设购进一辆事故车亏损![]() 元,一辆非事故车盈利
元,一辆非事故车盈利![]() 元:
元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进![]() 辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com