（1）请完成列联表；

（2）根据上表说明，能否有99%的把握认为该校大学生收看开幕会与性别有关？（结果精确到0.001）

附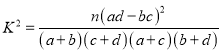：，其中.

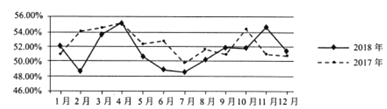
A. 2018年1月至4月的仓储指数比2017年同期波动性更大

B. 这两年的最大仓储指数都出现在4月份

C. 2018年全年仓储指数平均值明显低于2017年

D. 2018年各仓储指数的中位数与2017年各仓储指数中位数差异明显

【题目】已知椭圆C：1左右焦点为F1，F2直线（1）xy0与该椭圆有一个公共点在y轴上，另一个公共点的坐标为（m，1）．

（1）求椭圆C的方程；

（2）设P为椭圆C上任一点，过焦点F1，F2的弦分别为PM，PN，设λ1λ2，求λ1+λ2的值．

【题目】在平面角坐标系中，以坐标原点为极点， 轴的正半轴为极轴建立极坐标系，已知曲线的极坐标方程为，将曲线向左平移个单位长度得到曲线.

（1）求曲线的参数方程；

（2）已知为曲线上的动点， 两点的极坐标分别为，求的最大值.

【题目】设函数，．

（1）若曲线在点处的切线与轴平行，求；

（2）当时，函数的图象恒在轴上方，求的最大值．

【题目】已知椭圆的两个焦点分别为、，，点在椭圆上，且的周长为

（Ⅰ）求椭圆的方程；

（Ⅱ）若点的坐标为，不过原点的直线与椭圆相交于，两点，设线段的中点为，点到直线的距离为，且，，三点共线，求的最大值.

（1）设集合P＝{1，2，3}和Q＝{2，3，4，5}，分别从集合P和Q中随机取一个数作为a和b，求函数y＝f（x）在区间（﹣∞，2]上有零点且为减函数的概率？

（2）设集合P＝[1，3]和Q[2，5]，分别从集合P和Q中随机取一个实数作为a和b，求函数y＝f（x）在区间（﹣∞，2]上有零点且为减函数的概率？

【题目】已知椭圆C：1（a＞b＞0），椭圆C上的点到焦点距离的最大值为9，最小值为1．

（1）求椭圆C的标准方程；

（2）求椭圆C上的点到直线l：4x﹣5y+40＝0的最小距离？

【题目】如图，四棱锥中，底面ABCD，，，．

Ⅰ求证：平面PAC；

Ⅱ若侧棱PC上的点F满足，求三棱锥的体积．

【题目】如图，2012年春节，摄影爱好者S在某公园A处，发现正前方B处有一立柱，测得立柱顶端O的仰角和立柱底部B的俯角均为，已知S的身高约为米（将眼睛距地面的距离按米处理）

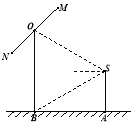
(1) 求摄影者到立柱的水平距离和立柱的高度；

(2) 立柱的顶端有一长2米的彩杆MN绕中点O在S与立柱所在的平面内旋转．摄影者有一视角范围为的镜头，在彩杆转动的任意时刻，摄影者是否都可以将彩杆全部摄入画面？说明理由．