
科目: 来源: 题型:
【题目】当前全世界人民越来越关注环境保护问题,某地某监测站点于2018年8月起连续n天监测空气质量指数(AQI),数据统计如下表:
空气质量指数(μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] |
空气质量等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 |
天数 | 20 | 40 | m | 10 | 5 |
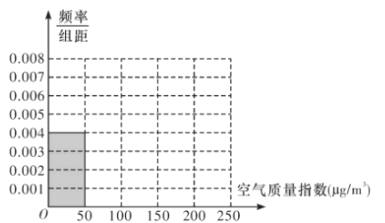
(1)根据所给统计表和频率分布直方图中的信息求出n,m的值,并完成频率分布直方图;
(2)由频率分布直方图,求该组数据的平均数与中位数;
(3)在空气质量指数分别为[0,50]和(50,100]的监测数据中,用分层抽样的方法抽取6天,从中任意选取2天,求事件A“两天空气质量等级都为良”发生的概率。
查看答案和解析>>
科目: 来源: 题型:
【题目】《九章算术》将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.下图所示的阳马![]() 中,侧棱
中,侧棱![]() 底面ABCD,且
底面ABCD,且![]() ,则当点E在下列四个位置:PA中点、PB中点、PC中点、PD中点时分别形成的四面体
,则当点E在下列四个位置:PA中点、PB中点、PC中点、PD中点时分别形成的四面体![]() 中,鳖臑有( )个.
中,鳖臑有( )个.
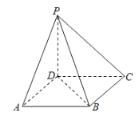
A.0B.1C.2D.3
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的长轴长为4,左、右顶点分别为
的长轴长为4,左、右顶点分别为![]() ,经过点
,经过点![]() 的动直线与椭圆
的动直线与椭圆![]() 相交于不同的两点
相交于不同的两点![]() (不与点
(不与点![]() 重合).
重合).
(1)求椭圆![]() 的方程及离心率;
的方程及离心率;
(2)求四边形![]() 面积的最大值;
面积的最大值;
(3)若直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,判断点
,判断点![]() 是否位于一条定直线上?若是,写出该直线的方程. (结论不要求证明)
是否位于一条定直线上?若是,写出该直线的方程. (结论不要求证明)
查看答案和解析>>
科目: 来源: 题型:
【题目】据报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改革”引起广泛关注,为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3 000人进行调查,就“是否取消英语听力”问题进行了问卷调查统计,结果如下表:
态度 | |||
调查人群 | 应该取消 | 应该保留 | 无所谓 |
在校学生 | 2100人 | 120人 | y人 |
社会人士 | 500人 | x人 | z人 |
已知在全体样本中随机抽取1人,抽到持“应该保留”态度的人的概率为0.06.
(1)现用分层抽样的方法在所有参与调查的人中抽取300人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“应该保留”态度的人中,用分层抽样的方法抽取6人,然后从这6人中随机抽取2人,求这2人中恰好有1个人为在校学生的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知曲线E的极坐标方程为4(ρ2-4)sin2θ=(16-ρ2)cos2θ,以极轴为x轴的非负半轴,极点O为坐标原点,建立平面直角坐标系.
(1)写出曲线E的直角坐标方程;
(2)若点P为曲线E上动点,点M为线段OP的中点,直线l的参数方程为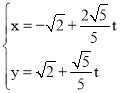 (t为参数),求点M到直线l的距离的最大值.
(t为参数),求点M到直线l的距离的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=![]() x3
x3![]() (a2+a+2)x2+a2(a+2)x,a∈R.
(a2+a+2)x2+a2(a+2)x,a∈R.
(1)当a=![]() 1时,求函数y=f(x)的单调区间;
1时,求函数y=f(x)的单调区间;
(2)求函数y=f(x)的极值点.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,四边形ABCD为平行四边形,△PCD为正三角形,∠BAD=30°,AD=4,AB=2![]() ,平面PCD⊥平面ABCD,E为PC中点.
,平面PCD⊥平面ABCD,E为PC中点.
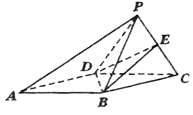
(1)证明:BE⊥PC;
(2)求多面体PABED的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com