①方程表示一个圆；

②若，则方程表示焦点在轴上的椭圆；

③已知点，若，则动点的轨迹是双曲线的右支；

④以过抛物线焦点的弦为直径的圆与该抛物线的准线相切，

其中正确说法的个数是（ ）

A.B.C.D.

【题目】现代城市大多是棋盘式布局（如北京道路几乎都是东西和南北走向）.在这样的城市中，我们说的两点间的距离往往不是指两点间的直线距离（位移），而是实际路程（如图）.在直角坐标平面内，我们定义，两点间的“直角距离”为：.

（1）在平面直角坐标系中，写出所有满足到原点的“直角距离”为2的“格点”的坐标.（格点指横、纵坐标均为整数的点）

（2）求到两定点、的“直角距离”和为定值的动点轨迹方程，并在直角坐标系内作出该动点的轨迹.（在以下三个条件中任选一个做答）

①，，；

②，，；

③，，.

（3）写出同时满足以下两个条件的“格点”的坐标，并说明理由（格点指横、纵坐标均为整数的点）.

①到，两点“直角距离”相等；

②到，两点“直角距离”和最小.

【题目】知函数．

（1）当时，求的单调区间；

（2）设函数，若是的唯一极值点，求．

【题目】已知双曲线的焦点，渐近线方程为，直线过点且与双曲线有且只有一个公共点.

（1）求双曲线的标准方程；

（2）求直线的方程.

【题目】已知抛物线过点，是抛物线上不同两点，且（其中是坐标原点），直线与交于点，线段的中点为.

（Ⅰ）求抛物线的准线方程；

（Ⅱ）求证：直线与轴平行.

【题目】如图，在多面体中，四边形为矩形，，均为等边三角形，，．

（1）过作截面与线段交于点，使得平面，试确定点的位置，并予以证明；

（2）在（1）的条件下，求直线与平面所成角的正弦值．

【题目】某快餐连锁店招聘外卖骑手，该快餐连锁店提供了两种日工资方案：方案①：规定每日底薪50元，快递业务每完成一单提成3元；方案②：规定每日底薪100元，快递业务的前44单没有提成，从第45单开始，每完成一单提成5元.该快餐连锁店记录了每天骑手的人均业务量.现随机抽取100天的数据，将样本数据分为，，，，，，七组，整理得到如图所示的频率分布直方图.

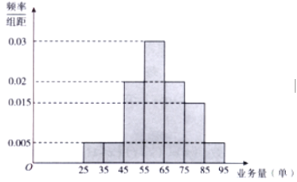
（1）随机选取一天，估计这一天该连锁店的骑手的人均日快递业务量不少于65单的概率；

（2）若骑手甲、乙选择了日工资方案①，丙、丁选择了日工资方案②.现从上述4名骑手中随机选取2人，求至少有1名骑手选择方案①的概率；

（3）若从人均日收入的角度考虑，请你利用所学的统计学知识为新聘骑手做出日工资方案的选择，并说明理由.（同组中的每个数据用该组区间的中点值代替）

A. 3 B. C. D. 2

【题目】如图，长方体中，，，点，，分别为，， 的中点，过点的平面与平面平行，且与长方体的面相交，交线围成一个几何图形.

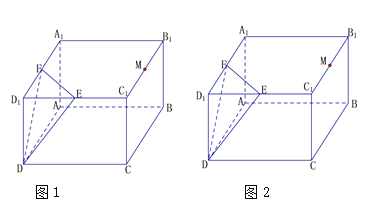
（1）在图1中，画出这个几何图形，并求这个几何图形的面积（不必说明画法与理由）；

（2）在图2中，求证：平面.

（1）请画出上表中年份代码与年销量的数据对应的散点图，并根据散点图判断.

与中哪一个更适宜作为年销售量关于年份代码的回归方程类型；

（2）根据（Ⅰ）的判断结果及表中数据，建立关于的回归方程，并预测2019年某新能源产品的销售量（精确到0.01）.

参考公式：，.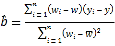

参考数据：，，，，，，，其中.