
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为侧棱
为侧棱![]() 上一点.
上一点.
(Ⅰ)若![]() ,求证:
,求证:![]()
![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)在侧棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出线段
?若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某隧道设计为双向四车道,车道总宽22米,要求通行车辆限高4.5米,隧道全长2.5千米,隧道的拱线近似地看成半个椭圆形状.

(1)若最大拱高h为6米,则隧道设计的拱宽l是多少?
(2)若最大拱高h不小于6米,则应如何设计拱高h和拱宽l,才能使半个椭圆形隧道的土方工程量最最小?(半个椭圆的面积公式为![]() ,柱体体积为:底面积乘以高.本题结果精确到0.1米)
,柱体体积为:底面积乘以高.本题结果精确到0.1米)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() 在双曲线
在双曲线![]()
![]() (
(![]() ,
,![]() )上,且双曲线的一条渐近线的方程是
)上,且双曲线的一条渐近线的方程是![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)若过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与双曲线
与双曲线![]() 有两个不同的交点,求实数
有两个不同的交点,求实数![]() 的取值范围;
的取值范围;
(3)设(2)中直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两个不同的点,若以线段
两个不同的点,若以线段![]() 为直径的圆经过坐标原点,求实数
为直径的圆经过坐标原点,求实数![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】改革开放40年来,体育产业蓬勃发展反映了“健康中国”理念的普及.下图是我国2006年至2016年体育产业年增加值及年增速图.其中条形图表示体育产业年增加值(单位:亿元),折线图为体育产业年增长率(%).
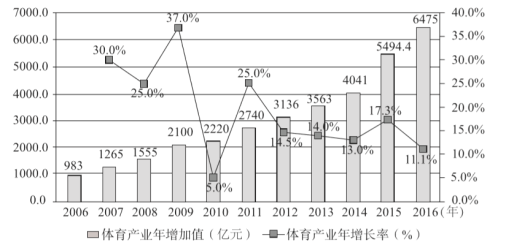
(Ⅰ)从2007年至2016年这十年中随机选出一年,求该年体育产业年增加值比前一年多![]() 亿元以上的概率;
亿元以上的概率;
(Ⅱ)从2007年至2011年这五年中随机选出两年,求至少有一年体育产业年增长率超过25%的概率;
(Ⅲ)由图判断,从哪年开始连续三年的体育产业年增长率方差最大?从哪年开始连续三年的体育产业年增加值方差最大?(结论不要求证明)
查看答案和解析>>
科目: 来源: 题型:
【题目】南北朝时代的伟大科学家祖暅在数学上有突出贡献,他在实践的基础上提出祖暅原理:“幂势既同,则积不容异”. 其含义是:夹在两个平行平面之间的两个几何体,被平行于这两个平行平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.如图,夹在两个平行平面之间的两个几何体的体积分别为![]() ,被平行于这两个平面的任意平面截得的两个截面面积分别为
,被平行于这两个平面的任意平面截得的两个截面面积分别为![]() ,则“
,则“![]() 相等”是“
相等”是“![]() 总相等”的
总相等”的

A. 充分而不必要条件B. 必要而不充分条件
C. 充分必要条件D. 既不充分也不必要条件
查看答案和解析>>
科目: 来源: 题型:
【题目】某林场现有木材存量为![]() ,每年以25%的增长率逐年递增,但每年年底要砍伐的木材量为
,每年以25%的增长率逐年递增,但每年年底要砍伐的木材量为![]() ,经过
,经过![]() 年后林场木材存有量为
年后林场木材存有量为![]()
(1)求![]() 的解析式
的解析式
(2)为保护生态环境,防止水土流失,该地区每年的森林木材存量不应少于![]() ,如果
,如果![]() ,那么该地区会发生水土流失吗?若会,要经过几年?(取
,那么该地区会发生水土流失吗?若会,要经过几年?(取![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com