
科目: 来源: 题型:
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直(其中
垂直(其中![]() 为自然对数的底数).
为自然对数的底数).
(1)求![]() 的解析式及单调递减区间;
的解析式及单调递减区间;
(2)是否存在常数![]() ,使得对于定义域内的任意
,使得对于定义域内的任意![]() ,
, ![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业为确定下一年投入某种产品的研发费用,需了解年研发费用![]() (单位:千万元)对年销售量
(单位:千万元)对年销售量![]() (单位:千万件)的影响,统计了近
(单位:千万件)的影响,统计了近![]() 年投入的年研发费用
年投入的年研发费用![]() 与年销售量
与年销售量![]() 的数据,得到散点图如图所示:
的数据,得到散点图如图所示:
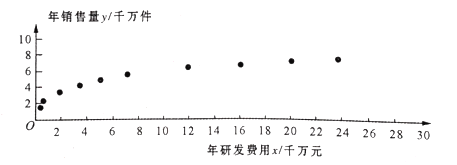
(Ⅰ)利用散点图判断,![]() 和
和![]() (其中
(其中![]() ,
,![]() 为大于
为大于![]() 的常数)哪一个更适合作为年研发费用
的常数)哪一个更适合作为年研发费用![]() 和年销售量
和年销售量![]() 的回归方程类型(只要给出判断即可,不必说明理由);
的回归方程类型(只要给出判断即可,不必说明理由);
(Ⅱ)对数据作出如下处理:令![]() ,
,![]() ,得到相关统计量的值如下表:
,得到相关统计量的值如下表:

根据(Ⅰ)的判断结果及表中数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅲ)已知企业年利润![]() (单位:千万元)与
(单位:千万元)与![]() ,
,![]() 的关系为
的关系为![]() (其中
(其中![]() ),根据(Ⅱ)的结果,要使得该企业下一年的年利润最大,预计下一年应投入多少研发费用?
),根据(Ⅱ)的结果,要使得该企业下一年的年利润最大,预计下一年应投入多少研发费用?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为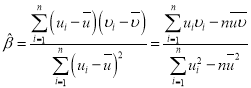 ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
附: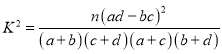
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
则下列说法正确的是( )
A.有![]() 以上的把握认为“爱好该项运动与性别无关”
以上的把握认为“爱好该项运动与性别无关”
B.有![]() 以上的把握认为“爱好该项运动与性别无关”
以上的把握认为“爱好该项运动与性别无关”
C.在犯错误的概率不超过![]() 的前提下,认为“爱好该项运动与性别有关”
的前提下,认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过![]() 的前提下,认为“爱好该项运动与性别有关”
的前提下,认为“爱好该项运动与性别有关”
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线C关于
中,抛物线C关于![]() 轴对称,顶点为坐标原点,且经过点
轴对称,顶点为坐标原点,且经过点![]() .
.
(1)求抛物线C的标准方程;
(2) 过点![]() 的直线交抛物线于M、N两点.是否存在定直线
的直线交抛物线于M、N两点.是否存在定直线![]() ,使得l上任意点P与点M,Q,N所成直线的斜率
,使得l上任意点P与点M,Q,N所成直线的斜率![]() ,
,![]() ,
,![]() 成等差数列.若存在,求出直线l的方程;若不存在,说明理由.
成等差数列.若存在,求出直线l的方程;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】十八届五中全会首次提出了绿色发展理念,将绿色发展作为“十三五”乃至更长时期经济社会发展的一个重要理念.某地区践行“绿水青山就是金山银山”的绿色发展理念,2015年初至2019年初,该地区绿化面积y(单位:平方公里)的数据如下表:
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号x | 1 | 2 | 3 | 4 | 5 |
绿化面积y | 2.8 | 3.5 | 4.3 | 4.7 | 5.2 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(2)利用(1)中的回归方程,预测该地区2025年初的绿化面积.
(参考公式:线性回归方程:![]() ,
,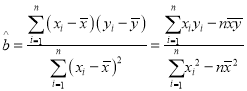 ,
,![]() 为数据平均数)
为数据平均数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com