
科目: 来源: 题型:
【题目】定义:若两个椭圆的离心率相等,则称两个椭圆是“相似”的.如图,椭圆![]() 与椭圆
与椭圆![]() 是相似的两个椭圆,并且相交于上下两个顶点,椭圆
是相似的两个椭圆,并且相交于上下两个顶点,椭圆![]() 的长轴长是4,椭圆
的长轴长是4,椭圆![]() 长轴长是2,点
长轴长是2,点![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左焦点与右焦点.
的左焦点与右焦点.

(1)求椭圆![]() ,
,![]() 的方程;
的方程;
(2)过![]() 的直线交椭圆
的直线交椭圆![]() 于点
于点![]() ,
,![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在第十五次全国国民阅读调查中,某地区调查组获得一个容量为![]() 的样本,其中城镇居民
的样本,其中城镇居民![]() 人,农村居民
人,农村居民![]() 人.在这些居民中,经常阅读的城镇居民
人.在这些居民中,经常阅读的城镇居民![]() 人,农村居民
人,农村居民![]() 人.
人.
(Ⅰ)填写下面列联表,并判断是否有![]() 的把握认为,经常阅读与居民居住地有关?
的把握认为,经常阅读与居民居住地有关?
城镇居民 | 农村居民 | 合计 | |
经常阅读 |
|
| |
不经常阅读 | |||
合计 |
|
(Ⅱ)从该地区居民城镇的居民中,随机抽取![]() 位居民参加一次阅读交流活动,记这
位居民参加一次阅读交流活动,记这![]() 位居民中经常阅读的人数为
位居民中经常阅读的人数为![]() ,若用样本的频率作为概率,求随机变量
,若用样本的频率作为概率,求随机变量![]() 的分布列和期望.
的分布列和期望.
附: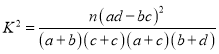 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴,焦距为2,且长轴长是短轴长的
轴,焦距为2,且长轴长是短轴长的![]() 倍.
倍.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() ,过椭圆
,过椭圆![]() 左焦点
左焦点![]() 的直线
的直线![]() 交
交![]() 于
于![]() 、
、![]() 两点,若对满足条件的任意直线
两点,若对满足条件的任意直线![]() ,不等式
,不等式![]() (
(![]() )恒成立,求
)恒成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.在购进机器时,可以一次性额外购买几次维修服务,每次维修服务费用200元,另外实际维修一次还需向维修人员支付小费,小费每次50元.在机器使用期间,如果维修次数超过购机时购买的维修服务次数,则每维修一次需支付维修服务费用500元,无需支付小费.现需决策在购买机器时应同时一次性购买几次维修服务,为此搜集并整理了100台这种机器在三年使用期内的维修次数,得下面统计表:
维修次数 | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 20 | 30 | 30 | 10 |
记x表示1台机器在三年使用期内的维修次数,y表示1台机器在维修上所需的费用(单位:元),![]() 表示购机的同时购买的维修服务次数.
表示购机的同时购买的维修服务次数.
(1)若![]() =10,求y与x的函数解析式;
=10,求y与x的函数解析式;
(2)若要求“维修次数不大于![]() ”的频率不小于0.8,求n的最小值;
”的频率不小于0.8,求n的最小值;
(3)假设这100台机器在购机的同时每台都购买10次维修服务,或每台都购买11次维修服务,分别计算这100台机器在维修上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买10次还是11次维修服务?
查看答案和解析>>
科目: 来源: 题型:
【题目】某分公司经销某种品牌产品,每件产品的成本为30元,并且每件产品须向总公司缴纳![]() 元(
元(![]() 为常数,
为常数,![]() )的管理费.根据多年的统计经验,预计当每件产品的售价为
)的管理费.根据多年的统计经验,预计当每件产品的售价为![]() 元时,产品一年的销售量为
元时,产品一年的销售量为![]() 为自然对数的底数)万件.已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价
为自然对数的底数)万件.已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价![]() 最低不低于35元,最高不超过41元.
最低不低于35元,最高不超过41元.
(Ⅰ)求分公司经营该产品一年的利润![]() 万元与每件产品的售价
万元与每件产品的售价![]() 元的函数关系式;
元的函数关系式;
(Ⅱ)当每件产品的售价为多少元时,该产品一年的利润![]() 最大,并求
最大,并求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校高一![]() 班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.
班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.

![]() 1
1![]() 求分数在
求分数在![]() 的频数及全班人数;
的频数及全班人数;
![]() 2
2![]() 求分数在
求分数在![]() 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中![]() 间矩形的高;
间矩形的高;
![]() 3
3![]() 若要从分数在
若要从分数在![]() 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在![]() 之间的概率.
之间的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,若函数
,若函数![]() 满足:①在区间
满足:①在区间![]() 上单调递减;②存在常数
上单调递减;②存在常数![]() ,使其值域为
,使其值域为![]() ,则称函数
,则称函数![]() 是函数
是函数![]() 的“渐近函数”.
的“渐近函数”.
(1)求证:函数![]() 不是函数
不是函数![]() 的“渐近函数”;
的“渐近函数”;
(2)判断函数![]() 是不是函数
是不是函数![]() ,
,![]() 的“渐近函数”,并说明理由;
的“渐近函数”,并说明理由;
(3)若函数![]() ,
,![]() ,
,![]() ,求证:
,求证:![]() 是函数
是函数![]() 的“渐近函数”充要条件是
的“渐近函数”充要条件是![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】下图是函数![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() )在区间
)在区间![]() 上的图象,为了得到这个函数的图象,只需将
上的图象,为了得到这个函数的图象,只需将![]() (
(![]() )的图像上所有的点( )
)的图像上所有的点( )

A. 向左平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
B. 向左平移![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的![]() 倍,纵坐标不变
倍,纵坐标不变
C. 向左平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
D. 向左平移![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的![]() 倍,纵坐标不变
倍,纵坐标不变
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com