【题目】李克强总理在2018年政府工作报告指出，要加快建设创新型国家，把握世界新一轮科技革命和产业变革大势，深入实施创新驱动发展战略，不断增强经济创新力和竞争力.某手机生产企业积极响应政府号召，大力研发新产品，争创世界名牌.为了对研发的一批最新款手机进行合理定价，将该款手机按事先拟定的价格进行试销，得到一组销售数据，如表所示：

已知.

（1）若变量具有线性相关关系，求产品销量（百件）关于试销单价（千元）的线性回归方程；

（2）用（1）中所求的线性回归方程得到与对应的产品销量的估计值.当销售数据对应的残差的绝对值时，则将销售数据称为一个“好数据”.现从个销售数据中任取个子，求“好数据”个数的分布列和数学期望.

（参考公式：线性回归方程中的估计值分别为.

【题目】如图，在三棱锥中，，侧面底面，，为线段上一点，且满足.

（1）若为的中点，求证：；

（2）当最小时，求二面角的余弦值.

【题目】设椭圆的左焦点为，上顶点为.已知椭圆的短轴长为4，离心率为.

（1）求椭圆的方程；

（2）设点在椭圆上，且异于椭圆的上、下顶点，点为直线与轴的交点，点在轴的负半轴上．若（为原点），且，求证：直线的斜率与直线MN的斜率之积为定值．

(1)求高一(1)班参加校生物竞赛的人数及分数在[80,90)之间的频数，并计算频率分布直方图中[80,90)间的矩形的高；

(2)若要从分数在[80,100]之间的学生中任选2人进行某项研究，求至少有1人分数在[90,100]之间的概率．

【题目】如图，已知是半圆的直径，，是将半圆圆周四等分的三个分点．

（1）从这5个点中任取3个点，求这3个点组成直角三角形的概率；

（2）在半圆内任取一点，求的面积大于的概率．

【题目】菜市房管局为了了解该市市民2018年1月至2019年1月期间购买二手房情况，首先随机抽样其中200名购房者，并对其购房面积（单位：平方米，）进行了一次调查统计，制成了如图1所示的频率分布南方匿，接着调查了该市2018年1月﹣2019年1月期间当月在售二手房均价（单位：万元/平方米），制成了如图2所示的散点图（图中月份代码1﹣13分别对应2018年1月至2019年1月）．

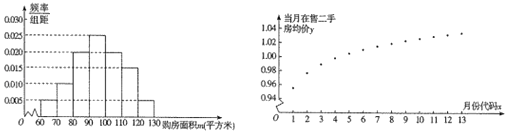
（1）试估计该市市民的平均购房面积．

（2）现采用分层抽样的方法从购房耐积位于的40位市民中随机取4人，再从这4人中随机抽取2人，求这2人的购房面积恰好有一人在的概率．

（3）根据散点图选择和两个模型进行拟合，经过数据处理得到两个回归方程，分别为和，并得到一些统计量的值，如表所示：

请利用相关指数判断哪个模型的拟合效果更好，并用拟合效果更好的模型预测2019年6月份的二手房购房均价（精确到）．

参考数据：，，，，,,,．参考公式：相关指数．

(1)求高一(1)班参加校生物竞赛的人数及分数在[80,90)之间的频数，并计算频率分布直方图中[80,90)间的矩形的高；

(2)若要从分数在[80,100]之间的学生中任选2人进行某项研究，求至少有1人分数在[90,100]之间的概率．

【题目】如图，已知是半圆的直径，，是将半圆圆周四等分的三个分点．

（1）从这5个点中任取3个点，求这3个点组成直角三角形的概率；

（2）在半圆内任取一点，求的面积大于的概率．

【题目】已知函数，若曲线在点处的切线方程是，不等式的解集为非空集合，其中为自然对数的底数.

（Ⅰ）求的解析式，并用表示；

（Ⅱ）若任意，不等式恒成立，求实数的取值范围.

【题目】已知分别是双曲线E： 的左、右焦点，P是双曲线上一点， 到左顶点的距离等于它到渐近线距离的2倍，（1）求双曲线的渐近线方程；（2）当时， 的面积为，求此双曲线的方程。