
科目: 来源: 题型:
【题目】某学校随机抽取部分学生调查其上学路上所需时间(单位:分钟),并将所得数据制成频率分布直方图(如图),若上学路上所需时间的范围为![]() ,样本数据分组为
,样本数据分组为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求直方图中a的值;
(2)如果上学路上所需时间不少于40分钟的学生可申请在学校住宿,若招收学生1200人,请估计所招学生中有多少人可以申请住宿;
(3)求该校学生上学路上所需的平均时间.
查看答案和解析>>
科目: 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn,若S9=81,a3+a5=14.
(1)求数列{an}的通项公式;
(2)设bn=![]() ,若{bn}的前n项和为Tn,证明:Tn<
,若{bn}的前n项和为Tn,证明:Tn<![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知棱长为1的正方体ABCD-A1B1C1D1中,E,F,M分别是线段AB、AD、AA1的中点,又P、Q分别在线段A1B1、A1D1上,且A1P=A1Q=x(0<x<1).设平面MEF∩平面MPQ
=l,现有下列结论:
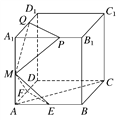
①l∥平面ABCD;
②l⊥AC;
③直线l与平面BCC1B1不垂直;
④当x变化时,l不是定直线.
其中不成立的结论是________.(写出所有不成立结论的序号)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 是坐标原点.
是坐标原点.
(1)若直线![]() 过点
过点![]() 且
且![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)已知点![]() ,若直线
,若直线![]() 不与坐标轴垂直,且
不与坐标轴垂直,且![]() ,证明:直线
,证明:直线![]() 过定点.
过定点.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() (
(![]() )经过点
)经过点![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 有两个不同的交点
有两个不同的交点![]() 、
、![]() ,直线
,直线![]() 交
交![]() 轴于
轴于![]() ,直线
,直线![]() 交
交![]() 轴于
轴于![]() .
.
(1)若直线![]() 过点
过点![]() ,求直线
,求直线![]() 的斜率的取值范围;
的斜率的取值范围;
(2)若直线![]() 过点
过点![]() ,设
,设![]() ,
,![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)若直线![]() 过抛物线
过抛物线![]() 的焦点
的焦点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题满分13分)
为回馈顾客,某商场拟通过摸球兑奖的方式对1000位顾客进行奖励,规定:每位顾客从一个装有4个标有面值的球的袋中一次性随机摸出2个球,球上所标的面值之和为该顾客所获的奖励额.
(1)若袋中所装的4个球中有1个所标的面值为50元,其余3个均为10元,求
①顾客所获的奖励额为60元的概率
②顾客所获的奖励额的分布列及数学期望;
(2)商场对奖励总额的预算是60000元,并规定袋中的4个球只能由标有面值10元和50元的两种球组成,或标有面值20元和40元的两种球组成.为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡,请对袋中的4个球的面值给出一个合适的设计,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴,离心率为
轴,离心率为![]() ,短轴长为2.
,短轴长为2.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() ,过椭圆
,过椭圆![]() 左焦点
左焦点![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,若对满足条件的任意直线
两点,若对满足条件的任意直线![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com