
科目: 来源: 题型:
【题目】2019年国际篮联篮球世界杯,将于2019年在北京、广州、南京、上海、武汉、深圳、佛山、东莞八座城市举行.为了宣传世界杯,某大学从全校学生中随机抽取了120名学生,对是否收看篮球世界杯赛事的情况进行了问卷调查,统计数据如下:

(1)根据上表说明,能否有![]() 的把握认为收看篮球世界杯赛事与性别有关?
的把握认为收看篮球世界杯赛事与性别有关?
(2)现从参与问卷调查的120名学生中,采用按性别分层抽样的方法选取6人参加2019年国际篮联篮球世界杯赛志愿者宣传活动.
(i)求男、女学生各选取多少人;
(ii)若从这6人中随机选取3人到校广播站开展2019年国际篮联篮球世界杯赛宣传介绍,求恰好选到2名男生的概率.
附: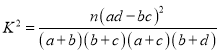 ,其中
,其中![]() .
.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() ,动点
,动点![]() 到直线
到直线![]() 的距离与动点
的距离与动点![]() 到点
到点![]() 的距离之比为
的距离之比为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 作任一直线交曲线
作任一直线交曲线![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 的垂线交直线
的垂线交直线![]() 于点
于点![]() ,求证:
,求证:![]() 平分线段
平分线段![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某部队在一次军演中要先后执行六项不同的任务,要求是:任务![]() 必须排在前三项执行,且执行任务
必须排在前三项执行,且执行任务![]() 之后需立即执行任务
之后需立即执行任务![]() ,任务
,任务![]() 、
、![]() 相邻,则不同的执行方案共有______种.
相邻,则不同的执行方案共有______种.
查看答案和解析>>
科目: 来源: 题型:
【题目】科研人员在对人体脂肪含量和年龄之间关系的研究中,获得了一些年龄和脂肪含量的简单随机样本数据,如下表:
| 26 | 27 | 39 | 41 | 49 | 53 | 56 | 58 | 60 | 61 |
| 14.5 | 17.8 | 21.2 | 25.9 | 26.3 | 29.6 | 31.4 | 33.5 | 35.2 | 34.6 |
根据上表的数据得到如下的散点图.
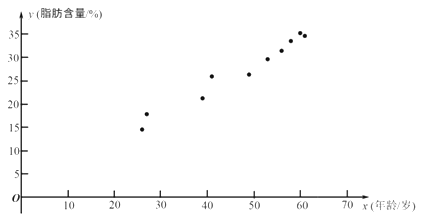
(1)根据上表中的样本数据及其散点图:
(i)求![]() ;
;
(i)计算样本相关系数(精确到0.01),并刻画它们的相关程度.
(2)若![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,求
,求![]() 的值(精确到0.01),并根据回归方程估计年龄为50岁时人体的脂肪含量.
的值(精确到0.01),并根据回归方程估计年龄为50岁时人体的脂肪含量.
附:参考数据:img src="http://thumb.zyjl.cn/Upload/2019/08/18/08/786210e5/SYS201908180802150104289801_ST/SYS201908180802150104289801_ST.007.png" width="51" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
参考公式:相关系数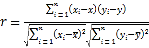
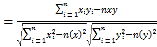
回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为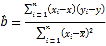 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】一商家诚邀甲、乙两名围棋高手进行一场网络国棋比赛,每比赛一局商家要向每名棋手支付2000元对局费,同时商家每局从转让网络转播权及广告宣传中获利12100元,从两名棋手以往比赛中得知,甲每局获胜的概率为![]() ,乙每局获胜的概率为
,乙每局获胜的概率为![]() ,两名棋手约定:最多下五局,先连胜两局者获胜,比赛结束,比赛结束后,商家为获胜者颁发5000元的奖金,若没有决出获胜者则各颁发2500元.
,两名棋手约定:最多下五局,先连胜两局者获胜,比赛结束,比赛结束后,商家为获胜者颁发5000元的奖金,若没有决出获胜者则各颁发2500元.
(1)求下完五局且甲获胜的概率是多少;
(2)求商家从这场网络棋赛中获得的收益的数学期望是多少.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面四边形![]() 中,
中,![]() 、
、![]() 分
分![]() 、
、![]() 所成的比为
所成的比为![]() ,即
,即![]() ,则有:
,则有:![]() .
.

(1)拓展到空间,写出空间四边形![]() 类似的命题,并加以证明;
类似的命题,并加以证明;
(2)在长方体![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,利用上述(1)的结论求线段
的中点,利用上述(1)的结论求线段![]() 的长度;
的长度;
(3)在所有棱长均为![]() 平行六面体
平行六面体![]() 中,
中,![]() (
(![]() 为锐角定值),
为锐角定值),![]() 、
、![]() 分
分![]() 、
、![]() 所成的比为
所成的比为![]() ,求
,求![]() 的长度.(用
的长度.(用![]() ,
,![]() ,
,![]() 表示)
表示)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知四棱锥![]() 的底面
的底面![]() 为菱形,且
为菱形,且![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .
.
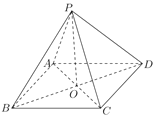
(1)求证:![]() 底面
底面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成的角
所成的角![]() 的值;
的值;
(3)求平面![]() 与平面
与平面![]() 所成二面角
所成二面角![]() 的值.(用反三角函数表示)
的值.(用反三角函数表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com