
科目: 来源: 题型:
【题目】随着人民生活水平的日益提高,某小区居民拥有私家车的数量与日俱增.由于该小区建成时间较早,没有配套建造地下停车场,小区内无序停放的车辆造成了交通的拥堵.该小区的物业公司统计了近五年小区登记在册的私家车数量(累计值,如124表示2016年小区登记在册的所有车辆数,其余意义相同),得到如下数据:
编号 | 1 | 2 | 3 | 4 | 5 |
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
数量 | 34 | 95 | 124 | 181 | 216 |
(1)若私家车的数量![]() 与年份编号
与年份编号![]() 满足线性相关关系,求
满足线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测2020年该小区的私家车数量;
的线性回归方程,并预测2020年该小区的私家车数量;
(2)小区于2018年底完成了基础设施改造,划设了120个停车位,为解决小区车辆乱停乱放的问题,加强小区管理,物业公司决定禁止无车位的车辆进入小区,由于车位有限,物业公司决定在2019年度采用网络竞拍的方式将车位对业主出租,租期一年,竞拍方案如下:
①截至2018年已登记在册的私家车业主拥有竞拍资格;
②每车至多申请一个车位,由车主在竞拍网站上提出申请并给出自己的报价;
③根据物价部门的规定,竞价不得超过1200元;
④申请阶段截止后,将所有申请的业主报价自高到低排列,排在前120位的业主以其报价成交;
⑤若最后出现并列的报价,则以提出申请的时间在前的业主成交,为预测本:次竞拍的成交最低价,物业公司随机抽取了有竞拍资格的40位业主进行竞拍意向的调查,统计了他们的拟报竞价,得到如下频率分布直方图:
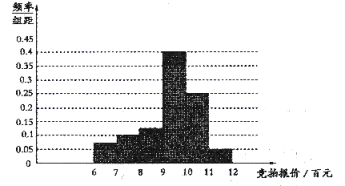
(ⅰ)求所抽取的业主中有意向竞拍报价不低于1000元的人数;
(ⅱ)如果所有符合条件的车主均参与竞拍,利用样木估计总体的思想,请你据此预测至少需要报价多少元才能竞拍车位成功?(精确到整数)
参考公式:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: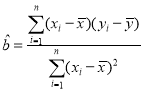
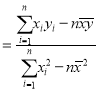 ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是2018年第一季度五省GDP情况图,则下列描述中不正确的是( )
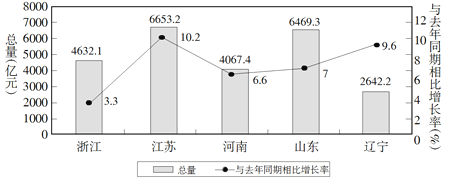
A. 与去年同期相比2018年第一季度五个省的GDP总量均实现了增长
B. 2018年第一季度GDP增速由高到低排位第5的是浙江省
C. 2018年第一季度GDP总量和增速由高到低排位均居同一位的省只有1个
D. 去年同期河南省的GDP总量不超过4000亿元
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C:![]() 的离心率
的离心率![]() ,椭圆C上的点到其左焦点的最大距离为
,椭圆C上的点到其左焦点的最大距离为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点A![]() 作直线
作直线![]() 与椭圆相交于点B,则
与椭圆相交于点B,则![]() 轴上是否存在点P,使得线段
轴上是否存在点P,使得线段![]() ,且
,且![]() ?若存在,求出点P坐标;否则请说明理由.
?若存在,求出点P坐标;否则请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】以下结论正确的个数是( )
①若数列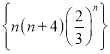 中的最大项是第
中的最大项是第![]() 项,则
项,则![]() .
.
②在![]() 中,若
中,若![]() ,则
,则![]() 为等腰直角三角形.
为等腰直角三角形.
③设![]() 、
、![]() 分别为等差数列
分别为等差数列![]() 与
与![]() 的前
的前![]() 项和,若
项和,若![]() ,则
,则![]() .
.
④![]() 的内角
的内角![]() 、
、![]() 、
、![]() 的对边分别为
的对边分别为![]() 、
、![]() 、
、![]() ,若
,若![]() 、
、![]() 、
、![]() 成等比数列,且
成等比数列,且![]() ,则
,则![]() .
.
⑤在![]() 中,
中,![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 所对边,
所对边,![]() ,则
,则![]() 的取值范围为
的取值范围为![]() .
.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】已知M为圆C:x2+y2-4x-14y+45=0上任意一点,且点Q(-2,3).
(1)求|MQ|的最大值和最小值;
(2)若M(m,n),求![]() 的最大值和最小值
的最大值和最小值
查看答案和解析>>
科目: 来源: 题型:
【题目】某合资企业招聘大学生时加试英语听力,待测试的小组中有男、女生共10人(其中女生人数多于男生人数),若从中随机选2人,其中恰为一男一女的概率为![]() .
.
(Ⅰ)求该小组中女生的人数;
(Ⅱ)若该小组中每个女生通过测试的概率均为![]() ,每个男生通过测试的概率均为
,每个男生通过测试的概率均为![]() .现对该小组中女生甲、女生乙和男生丙、丁4人进行测试.记这4人中通过测试的人数为随机变量X,求X的分布列和数学期望.
.现对该小组中女生甲、女生乙和男生丙、丁4人进行测试.记这4人中通过测试的人数为随机变量X,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com