【题目】已知函数（为自然对数的底数），是的导函数.

（Ⅰ）当时，求证；

（Ⅱ）是否存在正整数，使得对一切恒成立？若存在，求出的最大值；若不存在，说明理由.

【题目】已知点为椭圆的左焦点，且两焦点与短轴的一个顶点构成一个等边三角形，直线与椭圆有且仅有一个交点.

（Ⅰ）求椭圆的方程；

（Ⅱ）设直线与轴交于，过点的直线与椭圆交于两不同点，，若，求实数的取值范围.

【题目】设甲、乙两地相距400千米，汽车从甲地匀速行驶到乙地，速度不得超过100千米/小时，已知该汽车每小时的运输成本P(元)关于速度v（千米/小时）的函数关系是.

（1）求全程运输成本Q（元）关于速度v的函数关系式；

（2）为使全程运输成本最少，汽车应以多大速度行驶？并求此时运输成本的最小值.

【题目】椭圆的中心在原点，焦点在轴上，离心率，它的一个顶点恰好是抛物线的焦点.

（1）求椭圆的标准方程；

（2）过坐标原点的直线交椭圆于两点，在第一象限，轴，垂足为，连接延长交椭圆于点.

①求证：；

②求面积最大值.

设农科所确定的研究方案是：先从这五组数据中选取2组，用剩下的3组数据求线性回归方程，再对被选取的2组数据进行检验.

（参考：，）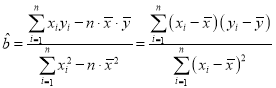

（1）若选取的是11月1日与11月5日的两组数据进行检验，请根据11月2日至11月4日的三组数据，求出关于的线性回归方程；

（2）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗，则认为得到的线性回归方程是可靠的，试问（1）中所得的线性回归方程是否可靠？

【题目】如图所示，在四棱台中，底面，四边形为菱形，，.

（1）若为中点，求证：平面；

（2）求直线与平面所成角的正弦值.

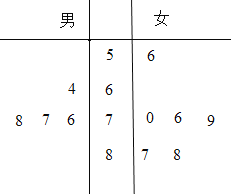
（1）根据这10名同学的测试成绩，估计该班男、女生国学素养测试的平均成绩；

（2）若成绩大于等于75分为优良，从这10名同学中随机选取2名男生，2名女生，求这4名同学的国学素养测试成绩均为优良的概率.

方案甲：员工最多有两次抽奖机会，每次抽奖的中奖率为.第一次抽奖，若未中奖，则抽奖结束.若中奖，则通过抛一枚质地均匀的硬币，决定是否继续进行第二次抽奖，规定：若抛出硬币，反面朝上，员工则获得500元奖金，不进行第二次抽奖；若正面朝上，员工则须进行第二次抽奖，且在第二次抽奖中，若中奖，获得奖金1000元；若未中奖，则所获奖金为0元.

方案乙：员工连续三次抽奖，每次中奖率均为，每次中奖均可获奖金400元.

（1）求某员工选择方案甲进行抽奖所获奖金（元）的分布列；

（2）某员工选择方案乙与选择方案甲进行抽奖，试比较哪个方案更划算？

【题目】已知函数.

（Ⅰ）求函数的极值点；

（Ⅱ）若直线过点，并且与曲线相切，求直线的方程；

（Ⅲ）设函数，其中，求函数在区间上的最小值.（其中为自然对数的底数）

【题目】已知数列的前n项和， 是等差数列，且.

（Ⅰ）求数列的通项公式；

（Ⅱ）令.求数列的前n项和.