
科目: 来源: 题型:
【题目】为了解春季昼夜温差大小与某种子发芽多少之间的关系,分别记录了4月1日至4月5日每天的昼夜温差与每天100颗种子浸泡后的发芽数,得到如下表格:
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 |
温差 | 12 | 11 | 13 | 10 | 8 |
发芽率 | 26 | 25 | 30 | 23 | 16 |
(1)从这5天中任选2天,求至少有一天种子发芽数超过25颗的概率;
(2)请根据4月1日、4月2日、4月3日这3天的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)根据(2)中所得的线性回归方程,预测温差为![]() 时,种子发芽的颗数.
时,种子发芽的颗数.
参考公式: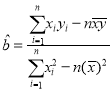 ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,其中
,其中![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 单调递增区间;
单调递增区间;
(2)求证:对任意![]() ,函数
,函数![]() 的图象在点
的图象在点![]() 处的切线恒过定点;
处的切线恒过定点;
(3)是否存在实数![]() 的值,使得
的值,使得![]() 在
在![]() 上有最大值或最小值,若存在,求出实数
上有最大值或最小值,若存在,求出实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
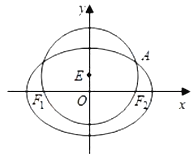
【题目】已知圆![]() :
: ![]() 经过椭圆
经过椭圆![]() :
: ![]() 的左右焦点
的左右焦点![]() ,且与椭圆
,且与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() 三点共线,直线
三点共线,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,且
两点,且![]() (
(![]() ).
).
(1)求椭圆![]() 的方程;
的方程;
(2)当三角形![]() 的面积取得最大值时,求直线
的面积取得最大值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】《九章算术》中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖騰.在如下图所示的阳马P-ABCD中,侧棱![]() 底面ABCD,且
底面ABCD,且![]() ,则当点E在下列四个位置:PA中点、PB中点、PC中点、PD中点时分别形成的四面体E-BCD中,鳖臑有( )
,则当点E在下列四个位置:PA中点、PB中点、PC中点、PD中点时分别形成的四面体E-BCD中,鳖臑有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 是边长为3的正方形,
是边长为3的正方形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,BE与平面
,BE与平面![]() 所成角为
所成角为![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)设点M在线段BD上,且![]() 平面BEF,求
平面BEF,求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知两点![]() ,
,![]() ,动点
,动点![]() 与
与![]() 两点连线的斜率
两点连线的斜率![]() 满足
满足![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)![]() 是曲线
是曲线![]() 与
与![]() 轴正半轴的交点,曲线
轴正半轴的交点,曲线![]() 上是否存在两点
上是否存在两点![]() ,使得
,使得![]() 是以
是以![]() 为直角顶点的等腰直角三角形?若存在,请说明有几个;若不存在,请说明理由.
为直角顶点的等腰直角三角形?若存在,请说明有几个;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() .
.
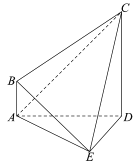
(1)求棱锥![]() 的体积;
的体积;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校为调查高二学生上学路程所需要的时间(单位:分钟),从高二年级学生中随机抽取![]() 名按上学所需要时间分组:第
名按上学所需要时间分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
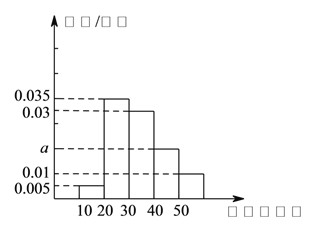
(![]() )根据图中数据求
)根据图中数据求![]() 的值.
的值.
(![]() )若从第
)若从第![]() ,
, ![]() ,
, ![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 名新生参与交通安全问卷调查,应从第
名新生参与交通安全问卷调查,应从第![]() ,
, ![]() ,
, ![]() 组各抽取多少名新生?
组各抽取多少名新生?
(![]() )在(
)在(![]() )的条件下,该校决定从这
)的条件下,该校决定从这![]() 名学生中随机抽取
名学生中随机抽取![]() 名新生参加交通安全宣传活动,求第
名新生参加交通安全宣传活动,求第![]() 组至少有一志愿者被抽中的概率.
组至少有一志愿者被抽中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com