
科目: 来源: 题型:
【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.如图是甲流水线样本的频数分布表和乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.如图是甲流水线样本的频数分布表和乙流水线样本的频率分布直方图.
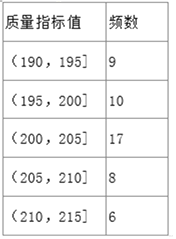
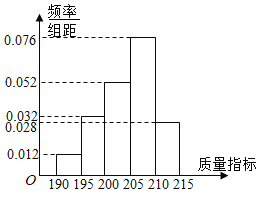
(1)根据频率分布直方图,估计乙流水线生产的产品该质量指标值的中位数;
(2)若将频率视为概率,某个月内甲、乙两条流水线均生产了5000件产品,则甲、乙两条流水线分别生产出不合格品约多少件?
(3)根据已知条件完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
的把握认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
甲流水线 | 乙流水线 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:![]() ,其中
,其中![]() .
.
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左右顶点是双曲线
的左右顶点是双曲线![]() 的顶点,且椭圆
的顶点,且椭圆![]() 的上顶点到双曲线
的上顶点到双曲线![]() 的渐近线的距离为
的渐近线的距离为![]() 。
。
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 相交于
相交于![]() 两点,与
两点,与![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】从某地区随机抽测120名成年女子的血清总蛋白含量(单位:![]() ),由测量结果得如图频数分布表:
),由测量结果得如图频数分布表:
(1)①仔细观察表中数据,算出该样本平均数![]() ______;
______;
②由表格可以认为,该地区成年女子的血清总蛋白含量Z服从正态分布![]() .其中
.其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本标准差s.经计算,该样本标准差
近似为样本标准差s.经计算,该样本标准差![]() .
.
医学上,Z过高或过低都为异常,Z的正常值范围通常取关于![]() 对称的区间
对称的区间![]() ,且Z位于该区间的概率为
,且Z位于该区间的概率为![]() ,试用该样本估计该地区血清总蛋白正常值范围.
,试用该样本估计该地区血清总蛋白正常值范围.
120名成年女人的血清总蛋白含量的频数分布表 | |||
分组 | 频数f | 区间中点值x |
|
| 2 | 65 | 130 |
| 8 | 67 | 536 |
| 12 | 69 | 828 |
| 15 | 71 | 1065 |
| 25 | 73 | 1825 |
| 24 | 75 | 1800 |
| 16 | 77 | 1232 |
| 10 | 79 | 790 |
| 7 | 81 | 567 |
| 1 | 83 | 83 |
合计 | 120 | 8856 | |
(2)结合(1)中的正常值范围,若该地区有5名成年女子检测血清总蛋白含量,测得数据分别为83.2,80,73,59.5,77,从中随机抽取2名女子,设血清总蛋白含量不在正常值范围的人数为X,求X的分布列和数学期望.
附:若![]() ,则
,则![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在一栋6层楼房里,每个房间的门牌号均为三位数,首位代表楼层号,后两位代表房间号,如218表示的是第2层第18号房间,现已知有宝箱藏在如下图18个房间里的某一间,其中甲同学只知道楼层号,乙同学只知道房间号,不知道楼层号,现有以下甲乙两人的一段对话:

甲同学说:我不知道,你肯定也不知道;
乙同学说:本来我也不知道,但是现在我知道了;
甲同学说:我也知道了.
根据上述对话,假设甲乙都能做出正确的推断,则藏有宝箱的房间的门牌号是______.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,若函数
时,若函数![]() 的导函数
的导函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
, ![]() 两点,其横坐标分别为
两点,其横坐标分别为![]() ,
, ![]() ,线段
,线段![]() 的中点的横坐标为
的中点的横坐标为![]() ,且
,且![]() ,
, ![]() 恰为函数
恰为函数![]() 的零点,求证:
的零点,求证: ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:极坐标与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求曲线![]() 的普通方程;
的普通方程;
(2)经过点![]() (平面直角坐标系
(平面直角坐标系![]() 中点)作直线
中点)作直线![]() 交曲线
交曲线![]() 于
于![]() ,
, ![]() 两点,若
两点,若![]() 恰好为线段
恰好为线段![]() 的三等分点,求直线
的三等分点,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在国家积极推动美丽乡村建设的政策背景下,各地根据当地生态资源打造了众多特色纷呈的乡村旅游胜地.某人意图将自己位于乡村旅游胜地的房子改造成民宿用于出租,在旅游淡季随机选取100天,对当地已有的六间不同价位的民宿进行跟踪,统计其出租率![]() (
(![]() ),设民宿租金为
),设民宿租金为![]() (单位:元/日),得到如图所示的数据散点图.
(单位:元/日),得到如图所示的数据散点图.
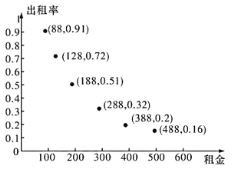
(1)若用“出租率”近似估计旅游淡季民宿每天租出去的概率,求租金为388元的那间民宿在淡季内的三天中至少有2天闲置的概率.
(2)①根据散点图判断,![]() 与
与![]() 哪个更适合于此模型(给出判断即可,不必说明理由)?根据判断结果求回归方程;
哪个更适合于此模型(给出判断即可,不必说明理由)?根据判断结果求回归方程;
②若该地一年中旅游淡季约为280天,在此期间无论民宿是否出租,每天都要付出![]() 的固定成本,若民宿出租,则每天需要再付出
的固定成本,若民宿出租,则每天需要再付出![]() 的日常支出成本.试用①中模型进行分析,旅游淡季民宿租金约定为多少元时,该民宿在这280天的收益
的日常支出成本.试用①中模型进行分析,旅游淡季民宿租金约定为多少元时,该民宿在这280天的收益![]() 达到最大?
达到最大?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ;
;![]() .
.
参考数据:记![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com