
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.直线
上.直线![]() 过点
过点![]() ,且与椭圆
,且与椭圆![]() 交于
交于![]() ,
,![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() .
.
(I)求椭圆![]() 的方程;
的方程;
(Ⅱ)点![]() 为坐标原点,延长线段
为坐标原点,延长线段![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,四边形
,四边形![]() 能否为平行四边形?若能,求出此时直线
能否为平行四边形?若能,求出此时直线![]() 的方程,若不能,说明理由.
的方程,若不能,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线![]() 不与坐标轴垂直,且与抛物线
不与坐标轴垂直,且与抛物线![]() 有且只有一个公共点
有且只有一个公共点![]() .
.
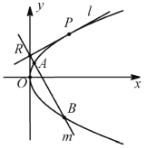
(1)当点![]() 的坐标为
的坐标为![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(2)设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,过点
,过点![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点.当
两点.当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】在四棱锥P﹣ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,PA![]() ,AC∩BD=O
,AC∩BD=O

(1)设平面ABP∩平面DCP=l,证明:l∥AB
(2)若E是PA的中点,求三棱锥P﹣BCE的体积VP﹣BCE.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,AB=2,∠BAD=60°,M是PD的中点.

(Ⅰ)求证:OM∥平面PAB;
(Ⅱ)平面PBD⊥平面PAC;
(Ⅲ)当三棱锥C﹣PBD的体积等于 ![]() 时,求PA的长.
时,求PA的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学有初中学生1800人,高中学生1200人. 为了解学生本学期课外阅读时间,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们课外阅读时间,然后按“初中学生”和“高中学生”分为两组,再将每组学生的阅读时间(单位:小时)分为5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并分别加以统计,得到如图所示的频率分布直方图.
,并分别加以统计,得到如图所示的频率分布直方图.
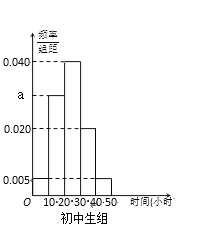
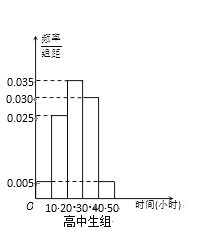
(Ⅰ)写出![]() 的值;试估计该校所有学生中,阅读时间不小于30个小时的学生人数;
的值;试估计该校所有学生中,阅读时间不小于30个小时的学生人数;
(Ⅱ)从阅读时间不足10个小时的样本学生中随机抽取2人,求至少抽到1名高中生的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,两焦点与短轴的一个端点的连线构成的三角形面积为
,两焦点与短轴的一个端点的连线构成的三角形面积为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设与圆O:![]() 相切的直线l交椭圆C于A,B两点(O为坐标原点),求△AOB面积的最大值。
相切的直线l交椭圆C于A,B两点(O为坐标原点),求△AOB面积的最大值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com