
科目: 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
,![]() ,点
,点![]() 为短轴的一个端点,
为短轴的一个端点,![]() .
.
(1)求椭圆C的方程;
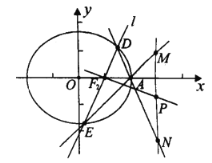
(2)如图,过右焦点![]() ,且斜率为k(
,且斜率为k(![]() )的直线l与椭圆C相交于D,E两点,A为椭圆的右顶点,直线
)的直线l与椭圆C相交于D,E两点,A为椭圆的右顶点,直线![]() ,
,![]() 分别交直线
分别交直线![]() 于点M,N,线段
于点M,N,线段![]() 的中点为P,记直线
的中点为P,记直线![]() 的斜率为
的斜率为![]() .试问
.试问![]() 是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
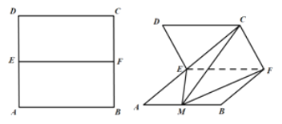
【题目】已知正方形的边长为4,E,F分别为![]() ,
,![]() 的中点,以
的中点,以![]() 为棱将正方形
为棱将正方形![]() 折成如图所示的
折成如图所示的![]() 的二面角,点M在线段
的二面角,点M在线段![]() 上.
上.
(1)若M为![]() 的中点,且直线
的中点,且直线![]() 与由A,D,E三点所确定平面的交点为G,试确定点G的位置,并证明直线
与由A,D,E三点所确定平面的交点为G,试确定点G的位置,并证明直线![]() 面
面![]() ;
;
(2)是否存在M,使得直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ;若存在,求此时
;若存在,求此时![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某“双一流![]() 类”大学就业部从该校2018年已就业的大学本科毕业生中随机抽取了100人进行问卷调查,其中一项是他们的月薪收入情况,调查发现,他们的月薪收入在人民币1.65万元到2.35万元之间,根据统计数据分组,得到如下的频率分布直方图:
类”大学就业部从该校2018年已就业的大学本科毕业生中随机抽取了100人进行问卷调查,其中一项是他们的月薪收入情况,调查发现,他们的月薪收入在人民币1.65万元到2.35万元之间,根据统计数据分组,得到如下的频率分布直方图:

(1)将同一组数据用该区间的中点值作代表,求这100人月薪收入的样本平均数![]() ;
;
(2)该校在某地区就业的2018届本科毕业生共50人,决定于2019国庆长假期间举办一次同学联谊会,并收取一定的活动费用,有两种收费方案:
方案一:设区间![]() ,月薪落在区间
,月薪落在区间![]() 左侧的每人收取400元,月薪落在区间
左侧的每人收取400元,月薪落在区间![]() 内的每人收取600元,月薪落在区间
内的每人收取600元,月薪落在区间![]() 右侧的每人收取800元;
右侧的每人收取800元;
方案二:每人按月薪收入的样本平均数的![]() 收取;
收取;
用该校就业部统计的这100人月薪收入的样本频率进行估算,哪一种收费方案能收到更多的费用?
查看答案和解析>>
科目: 来源: 题型:
【题目】袋子中有四个小球,分别写有“四”“校”“联”“考”四个字,有放回地从中任取一个小球,取到“联”就停止,用随机模拟的方法估计直到第二次停止的概率:先由计算器产生1到4之间取整数值的随机数,且用1,2,3,4表示取出小球上分别写有“四”“校”“联”“考”四个字,以每两个随机数为一组,代表两次的结果,经随机模拟产生了20组随机数:13 24 12 32 43 14 24 32 31 21 23 13 32 21 24 42 13 32 23 34据此估计,直到第二次就停止的概率为______.
查看答案和解析>>
科目: 来源: 题型:
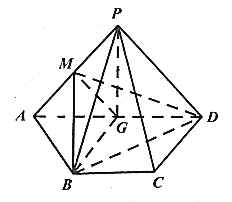
【题目】利用一半径为4cm的圆形纸片(圆心为O)制作一个正四棱锥.方法如下:
(1)以O为圆心制作一个小的圆;
(2)在小的圆内制作一内接正方形ABCD;
(3)以正方形ABCD的各边向外作等腰三角形,使等腰三角形的顶点落在大圆上(如图);
(4)将正方形ABCD作为正四棱锥的底,四个等腰三角形作为正四棱锥的侧面折起,使四个等腰三角形的顶点重合,问:要使所制作的正四棱锥体积最大,则小圆的半径为

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,直线l:y![]() x﹣3经过椭圆
x﹣3经过椭圆![]() 1(a>b>0)的一个焦点,且点(0,b)到直线l的距离为2.
1(a>b>0)的一个焦点,且点(0,b)到直线l的距离为2.
(1)求椭圆E的方程;
(2)A、B、C是椭圆E上的三个动点,A与B关于原点对称,且|CA|=|CB|,求△ABC面积的最小值,并求此时点C的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知四边形![]() 的直角梯形,
的直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 平面
平面![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点(
上一点(![]() 不与端点重合).
不与端点重合).
(Ⅰ)若![]() ,
,
(i)求证:![]() 平面
平面![]() ;
;
(ii)求直线![]() 与平面
与平面![]() 所成的角的大小;
所成的角的大小;
(Ⅱ)否存在实数![]() 满足
满足![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成的锐角为
所成的锐角为![]() ,若存在,确定
,若存在,确定![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com