①若p是q的充分不必要条件，则￢p是￢q的必要不充分条件；

②若命题p：x≥0，x2+1＞0，则￢p：x0＜0，x02+1≤0；

③在△ABC中，A＞B是sinA＞sinB的充要条件；

④命题：当1＜t＜4时方程1表示焦点在x轴上的椭圆，为真命题．

其中真命题的序号是_____．

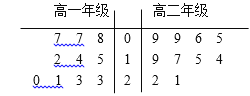
(Ⅰ) 从两个年级的参赛志愿者中各抽取两人，求抽取的4人中至少一人优秀的概率；

(Ⅱ) 从高一10名志愿者中抽取一人，高二10名志愿者中抽取两人，3人中优秀人数记为，求的分布列和数学期望.

A. 命题：“若，则”的逆否命题是“若，则”

B. “”是“”的充分不必要条件

C. 命题：“， ”的否定是“， ”

D. 若“”为假命题，则均为假命题

【题目】设函数.

(Ⅰ) 求曲线在点处的切线方程；

(Ⅱ) 讨论函数的单调性；

(Ⅲ) 设,当时,若对任意的，存在，使得≥，求实数的取值范围.

（1）求的值；

（2）分别求出甲、乙两组数据的方差和，并由此分析两组技工的加工水平；

【题目】已知数列的前n项和， 是等差数列，且.

（Ⅰ）求数列的通项公式；

（Ⅱ）令.求数列的前n项和.

【题目】2019年的流感来得要比往年更猛烈一些据四川电视台“新闻现场”播报，近日四川省人民医院一天的最高接诊量超过了一万四千人，成都市妇女儿童中心医院接诊量每天都在九千人次以上这些浩浩荡荡的看病大军中，有不少人都是因为感冒来的医院某课外兴趣小组趁着寒假假期空闲，欲研究昼夜温差大小与患感冒人数之间的关系，他们分别到成都市气象局与跳伞塔社区医院抄录了去年1到6月每月20日的昼夜温差情况与患感冒就诊的人数，得到如下资料：

该兴趣小组确定的研究方案是：先从这六组数据中选取2组，用剩下的4组数据求线性回归方程，再用被选取的2组数据进行检验．

若选取的是1月与6月的两组数据，请根据2月至5月份的数据，求出y关于x的线性回归方程；

若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人，则认为得到的线性回归方程是理想的，试问该小组所得线性回归方程是否理想？

参考公式： ，

【题目】如图，四棱锥的底面是菱形，底面，分别是的中点，，，.

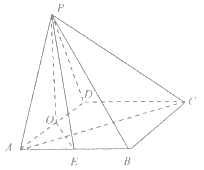
（I）证明：；

（II）求直线与平面所成角的正弦值；

（III）在边上是否存在点，使与所成角的余弦值为，若存在，确定点位置；若不存在，说明理由.

【题目】点外卖现已成为上班族解决午餐问题的一种流行趋势.某配餐店为扩大品牌影响力，决定对新顾客实行让利促销，规定：凡点餐的新顾客均可获赠10元或者16元代金券一张，中奖率分别为和，每人限点一餐，且100%中奖.现有A公司甲、乙、丙、丁四位员工决定点餐试吃.

(Ⅰ) 求这四人中至多一人抽到16元代金券的概率；

(Ⅱ) 这四人中抽到10元、16元代金券的人数分别用、表示，记，求随机变量的分布列和数学期望.

【题目】某公司采用招考方式引进人才，规定必须在、、三个测试点中任意选取两个进行测试，若在这两个测试点都测试合格，则可参加面试，否则不被录用，已知考生在每个测试点测试结果互不影响，若考生小李和小王一起前来参加招考，小李在测试点、、测试合格的概率分别为、、，小王在上述三个测试点测试合格的概率都是.

（1）问小李选择哪两个测试点测试才能使得可以参加面试的可能性最大？请说明理由；

（2）假设小李选择测试点、进行测试，小王选择测试点、进行测试，记为两人在各测试点测试合格的测试点个数之和，求随机变量的分布列及数学期望.