
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点A为椭圆的右顶点,点B为椭圆的上顶点,点F为椭圆的左焦点,且
,点A为椭圆的右顶点,点B为椭圆的上顶点,点F为椭圆的左焦点,且![]() 的面积是
的面积是![]() .
.
Ⅰ.求椭圆C的方程;
Ⅱ.设直线![]() 与椭圆C交于P、Q两点,点P关于x轴的对称点为
与椭圆C交于P、Q两点,点P关于x轴的对称点为![]() (
(![]() 与
与![]() 不重合),则直线
不重合),则直线![]() 与x轴交于点H,求
与x轴交于点H,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】若数列![]() 对任意
对任意![]() 满足
满足![]() ,下面给出关于数列
,下面给出关于数列![]() 的四个命题:①
的四个命题:①![]() 可以是等差数列,②
可以是等差数列,②![]() 可以是等比数列;③
可以是等比数列;③![]() 可以既是等差又是等比数列;④
可以既是等差又是等比数列;④![]() 可以既不是等差又不是等比数列;则上述命题中,正确的个数为( )
可以既不是等差又不是等比数列;则上述命题中,正确的个数为( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】“五一”期间,甲乙两个商场分别开展促销活动.
(Ⅰ)甲商场的规则是:凡购物满100元,可抽奖一次,从装有大小、形状相同的4个白球、4个黑球的袋中摸出4个球,中奖情况如下表:
摸出的结果 | 获得奖金(单位:元) |
4个白球或4个黑球 | 200 |
3个白球1个黑球或3个黑球1个白球 | 20 |
2个黑球2个白球 | 10 |
记![]() 为抽奖一次获得的奖金,求
为抽奖一次获得的奖金,求![]() 的分布列和期望.
的分布列和期望.
(Ⅱ)乙商场的规则是:凡购物满100元,可抽奖10次.其中,第![]() 次抽奖方法是:从编号为
次抽奖方法是:从编号为![]() 的袋中(装有大小、形状相同的
的袋中(装有大小、形状相同的![]() 个白球和
个白球和![]() 个黑球)摸出
个黑球)摸出![]() 个球,若该次摸出的
个球,若该次摸出的![]() 个球颜色都相同,则可获得奖金
个球颜色都相同,则可获得奖金![]() 元;记第
元;记第![]() 次获奖概率
次获奖概率![]() .设各次摸奖的结果互不影响,最终所获得的总奖金为10次奖金之和.
.设各次摸奖的结果互不影响,最终所获得的总奖金为10次奖金之和.
①求证:![]() ;
;
②若某顾客购买120元的商品,不考虑其它因素,从获得奖金的期望分析,他应该选择哪一家商场?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形![]() 是正方形,
是正方形,![]() 平面
平面![]() ,
,![]() 分别为
分别为![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的大小;
所成锐二面角的大小;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]() ?若存在,求出线段
?若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两台机床生产同一型号零件,记生产的零件的尺寸为![]() ,相关行业质检部门规定:若
,相关行业质检部门规定:若![]() ,则该零件为优等品;若
,则该零件为优等品;若![]() ,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质里检测得到下表数据:
,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质里检测得到下表数据:
尺寸 |
|
|
|
|
|
|
甲机床零件频数 | 2 | 3 | 20 | 20 | 4 | 1 |
乙机床零件频数 | 3 | 5 | 17 | 13 | 8 | 4 |
(Ⅰ)设生产每件产品的利润为:优等品3元,中等品1元,次品亏本1元.若将频率视为概率,试估算甲机床生产一件零件的利润的数学期望;
(Ⅱ)根据已知条件完成下面的列联表,并据此数据回答:是否有![]() 的把握认为“零件优等与否和所用机床有关”?
的把握认为“零件优等与否和所用机床有关”?
甲机床 | 乙机床 | 合计 | |
优等品 | |||
非优等品 | |||
合计 |
查看答案和解析>>
科目: 来源: 题型:
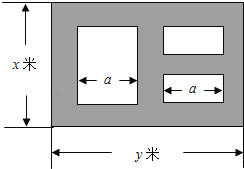
【题目】某市近郊有一块大约![]() 的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为
的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为![]() 平方米.
平方米.
(1)分别用![]() 表示
表示![]() 和
和![]() 的函数关系式,并给出定义域;
的函数关系式,并给出定义域;
(2)怎样设计能使![]() 取得最大值,并求出最大值.
取得最大值,并求出最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,点
,点![]() 满足
满足![]() ,记点
,记点![]() 的轨迹为
的轨迹为![]() .斜率为
.斜率为![]() 的直线
的直线![]() 过点
过点![]() ,且与轨迹
,且与轨迹![]() 相交于
相交于![]() 两点.
两点.
(1)求轨迹![]() 的方程;
的方程;
(2)求斜率![]() 的取值范围;
的取值范围;
(3)在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得无论直线
,使得无论直线![]() 绕点
绕点![]() 怎样转动,总有
怎样转动,总有![]() 成立?如果存在,求出定点
成立?如果存在,求出定点![]() ;如果不存在,请说明理由.
;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,直线
,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,且
,且![]() 是
是![]() 的中点.
的中点.
(Ⅰ)求椭圆的离心率;
(Ⅱ)过点![]() 的直线与椭圆相交于
的直线与椭圆相交于![]() 两点,
两点,![]() 都在
都在![]() 轴上方,并且
轴上方,并且![]() 在
在![]() 之间,且
之间,且![]() 到直线
到直线![]() 的距离是
的距离是![]() 到直线
到直线![]() 距离的
距离的![]() 倍.
倍.
①记![]() 的面积分别为
的面积分别为![]() ,求
,求![]() ;
;
②若原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求椭圆方程.
,求椭圆方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com