
科目: 来源: 题型:
【题目】下列四个结论:
![]() 两条直线和同一个平面垂直,则这两条直线平行;
两条直线和同一个平面垂直,则这两条直线平行;
![]() 两条直线没有公共点,则这两条直线平行;
两条直线没有公共点,则这两条直线平行;
![]() 两条直线都和第三条直线垂直,则这两条直线平行;
两条直线都和第三条直线垂直,则这两条直线平行;
![]() 一条直线和一个平面内任意直线没有公共点,则这条直线和这个平面平行.
一条直线和一个平面内任意直线没有公共点,则这条直线和这个平面平行.
其中正确的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,长轴是短轴的
,长轴是短轴的![]() 倍,且椭圆
倍,且椭圆![]() 过点
过点![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 过点
过点![]() ,坐标平面上的点
,坐标平面上的点![]() 满足到直线
满足到直线![]() 的距离为定值
的距离为定值![]() .
.
(1)写出椭圆![]() 方程;
方程;
(2)若椭圆![]() 上恰好存在
上恰好存在![]() 个这样的点
个这样的点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着移动互联网的发展,与餐饮美食相关的手机APP软件层出不穷.现从使用A和B两款订餐软件的商家中分别随机抽取50个商家,对它们的“平均送达时间”进行统计,得到频率分布直方图如图.
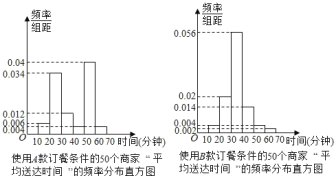
(1)试估计使用A款订餐软件的50个商家的“平均送达时间”的众数及平均数;
(2)根据以上抽样调查数据,回答以下问题:
(ⅰ)为了解如何降低各商家的送餐时间,我们先从这100家商家里选出平均送达时间不超过20分钟的商家,然后再从中随机挑选两家进行跟踪研究,求恰好所抽中的商家均为使用B款软件的概率.
(ⅱ)如果你要从A和B两款订餐软件中选择一款订餐,你会选择哪款?并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF||AB,AB=2,BC=EF=1,AE=![]() ,DE=3,∠BAD=60,G为BC的中点.
,DE=3,∠BAD=60,G为BC的中点.
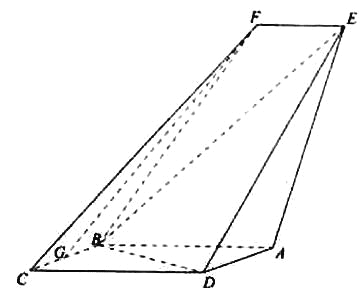
(Ⅰ)求证:FG||平面BED;
(Ⅱ)求证:平面BED⊥平面AED;
(Ⅲ)求直线EF与平面BED所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为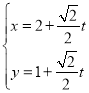 (
(![]() 为参数).
为参数).
(Ⅰ)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的值,并求定点
的值,并求定点![]() 到
到![]() ,
,![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目: 来源: 题型:
【题目】若函数![]() 满足:对于任意正数
满足:对于任意正数![]() ,都有
,都有![]() ,且
,且![]() ,则称函数
,则称函数![]() 为“L函数”.
为“L函数”.
(1)试判断函数![]() 与
与![]() 是否是“L函数”;
是否是“L函数”;
(2)若函数![]() 为“L函数”,求实数a的取值范围;
为“L函数”,求实数a的取值范围;
(3)若函数![]() 为“L函数”,且
为“L函数”,且![]() ,求证:对任意
,求证:对任意![]() ,都有
,都有![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在下列命题中,正确命题的序号为 (写出所有正确命题的序号).
①函数![]() 的最小值为
的最小值为![]() ;
;
②已知定义在![]() 上周期为4的函数
上周期为4的函数![]() 满足
满足![]() ,则
,则![]() 一定为偶函数;
一定为偶函数;
③定义在![]() 上的函数
上的函数![]() 既是奇函数又是以2为周期的周期函数,则
既是奇函数又是以2为周期的周期函数,则![]() ;
;
④已知函数![]() ,则
,则![]() 是
是![]() 有极值的必要不充分条件;
有极值的必要不充分条件;
⑤已知函数![]() ,若
,若![]() ,则
,则![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知焦距为2![]() 的椭圆
的椭圆![]() :
:![]() 的右顶点为
的右顶点为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 的左边),
的左边),![]() 在
在![]() 轴上的射影为
轴上的射影为![]() ,且四边形
,且四边形![]() 是平行四边形.
是平行四边形.
(1)求椭圆![]() 的方程;
的方程;
(2)斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两个不同的点
交于两个不同的点![]() ,
,![]() .
.
(i)若直线![]() 过原点且与坐标轴不重合,
过原点且与坐标轴不重合,![]() 是直线
是直线![]() 上一点,且
上一点,且![]() 是以
是以![]() 为直角顶点的等腰直角三角形,求
为直角顶点的等腰直角三角形,求![]() 的值;
的值;
(ii)若![]() 是椭圆的左顶点,
是椭圆的左顶点,![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,点
,点![]() 是
是![]() 轴上异于点
轴上异于点![]() 的点,且以
的点,且以![]() 为直径的圆恒过直线
为直径的圆恒过直线![]() 和
和![]() 的交点,求证:点
的交点,求证:点![]() 是定点.
是定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com