
科目: 来源: 题型:
【题目】![]() 年以来精准扶贫政策的落实,使我国扶贫工作有了新进展,贫困发生率由
年以来精准扶贫政策的落实,使我国扶贫工作有了新进展,贫困发生率由![]() 年底的
年底的![]() 下降到
下降到![]() 年底的
年底的![]() ,创造了人类减贫史上的的中国奇迹.“贫困发生率”是指低于贫困线的人口占全体人口的比例,
,创造了人类减贫史上的的中国奇迹.“贫困发生率”是指低于贫困线的人口占全体人口的比例,![]() 年至
年至![]() 年我国贫困发生率的数据如下表:
年我国贫困发生率的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
贫困发生率 | 10.2 | 8.5 | 7.2 | 5.7 | 4.5 | 3.1 | 1.4 |
(1)从表中所给的![]() 个贫困发生率数据中任选两个,求两个都低于
个贫困发生率数据中任选两个,求两个都低于![]() 的概率;
的概率;
(2)设年份代码![]() ,利用线性回归方程,分析
,利用线性回归方程,分析![]() span>年至
span>年至![]() 年贫困发生率
年贫困发生率![]() 与年份代码
与年份代码![]() 的相关情况,并预测
的相关情况,并预测![]() 年贫困发生率.
年贫困发生率.
附:回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为:
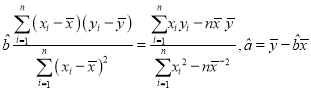 (
(![]() 的值保留到小数点后三位)
的值保留到小数点后三位)
查看答案和解析>>
科目: 来源: 题型:
【题目】如果函数![]() 的定义域为
的定义域为![]() ,且存在实常数
,且存在实常数![]() ,使得对于定义域内任意
,使得对于定义域内任意![]() ,都有
,都有![]() 成立,则称此函数
成立,则称此函数![]() 具有“性质
具有“性质![]() ”.
”.
(1)判断函数![]() 是否具有“
是否具有“![]() 性质”,若具有“
性质”,若具有“![]() 性质”,求出所有
性质”,求出所有![]() 的值的集合,若不具有“
的值的集合,若不具有“![]() 性质”,请说明理由;
性质”,请说明理由;
(2)已知函数![]() 具有“
具有“![]() 性质”,且当
性质”,且当![]() 时,
时,![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的值域;
上的值域;
(3)已知函数![]() 既具有“
既具有“![]() 性质”,又具有“
性质”,又具有“![]() 性质”,且当
性质”,且当![]() 时,
时,![]() ,若函数
,若函数![]() 的图像与直线
的图像与直线![]() 有2017个公共点,求实数
有2017个公共点,求实数![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】椭圆![]() 的顶点为
的顶点为![]() ,左、右焦点分别为
,左、右焦点分别为![]() 、
、![]() ,过点A且斜率为
,过点A且斜率为![]() 的直线与y轴交于点P,与椭圆交于另一个点B,且点B在x轴上的射影恰好为点
的直线与y轴交于点P,与椭圆交于另一个点B,且点B在x轴上的射影恰好为点![]() .
.
(1)求椭圆C的标准方程;
(2)M为椭圆C上一动点,![]() 是椭圆C长轴上的一个点,直线MQ与椭圆C的另一个交点为N,令
是椭圆C长轴上的一个点,直线MQ与椭圆C的另一个交点为N,令![]() ,若t值与点M的位置无关,则称此时的点Q为“稳定点”,试求出所有“稳定点”,若没有,请说明理由.
,若t值与点M的位置无关,则称此时的点Q为“稳定点”,试求出所有“稳定点”,若没有,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计,频率分布直方图如图所示:
(单位:克)中,经统计,频率分布直方图如图所示:
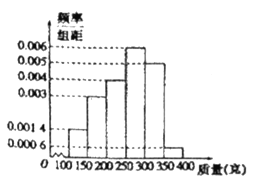
(1)估计这组数据的平均数(同一组中的数据以这组数据所在区间中点的值作代表);
(2)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取5个,再从这5个中随机抽取2个,求这2个芒果都来自同一个质量区间的概率;
的芒果中随机抽取5个,再从这5个中随机抽取2个,求这2个芒果都来自同一个质量区间的概率;
(3)某经销商来收购芒果,同一组中的数据以这组数据所在区间中点的值作代表,用样本估计总体,该种植园中还未摘下的芒果大约还有1000个,经销商提出以下两种收购方案:
方案①:所有芒果以9元/千克收购
方案②:对质量低于250克的芒果以2元/个收购,对质量高于或等于250克的芒果以3元/个收购.通过计算确定种植园选择哪种方案获利更多.
参考数据:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知定义在区间![]() 上两个函数
上两个函数![]() 和
和![]() ,
,![]() ,
,![]()
![]() ,
,![]() .
.
(1)求函数![]() 的最大值
的最大值![]() ;
;
(2)若![]() 在区间
在区间![]() 单调,求实数
单调,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,若对于任意
时,若对于任意![]() ,总存在
,总存在![]() ,使
,使![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增长该地一建设银行统计连续五年的储蓄存款(年底余额)得到下表:
年份x | 2014 | 2015 | 2016 | 2017 | 2018 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
为便于计算,工作人员将上表的数据进行了处理(令![]()
![]() ),得到下表:
),得到下表:
时间t | 1 | 2 | 3 | 4 | 5 |
储蓄存款z | 0 | 1 | 2 | 3 | 5 |
(1)求z关于t的线性回归方程;
(2)通过(1)中的方程,求出y关于x的回归方程;
(3)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
附:线性回归方程![]() ,其中
,其中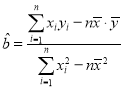 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】勒洛三角形是具有类似圆的“定宽性”的面积最小的曲线,它由德国机械工程专家,机构运动学家勒洛首先发现,其作法是:以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,三段弧围成的曲边三角形就是勒洛三角形,现在勒洛三角形中随机取一点,则此点取自正三角形外的概率为( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义域和值域均为![]() (常数
(常数![]() )的函数
)的函数![]() 和y=g(x)的图像如图所示,给出下列四个命题:
和y=g(x)的图像如图所示,给出下列四个命题:
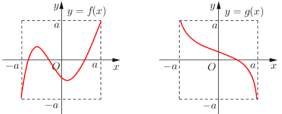
(1)方程![]() 有且仅有三个解;
有且仅有三个解;
(2)方程![]() 有且仅有三个解;
有且仅有三个解;
(3)方程![]() 有且仅有九个解;
有且仅有九个解;
(4)方程![]() 有且仅有一个解;
有且仅有一个解;
那么,其中正确命题的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】设单调函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,如果单调函数
,如果单调函数![]() 使得函数
使得函数![]() 的值域也是
的值域也是![]() ,则称函数
,则称函数![]() 是函数
是函数![]() 的一个“保值域函数”.已知定义域为
的一个“保值域函数”.已知定义域为![]() 的函数
的函数![]() ,函数
,函数![]() 与
与![]() 互为反函数,且
互为反函数,且![]() 是
是![]() 的一个“保值域函数”,
的一个“保值域函数”,![]() 是
是![]() 的一个“保值域函数”,则
的一个“保值域函数”,则![]() __________.
__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com