
科目: 来源: 题型:
【题目】定义![]() 为不超过
为不超过![]() 的最大整数,例如
的最大整数,例如![]() ,
,![]() .已知
.已知![]() 是等比数列,若
是等比数列,若![]() ,且前
,且前![]() 项和为
项和为![]() .
.
(1)若不等式![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)求![]() 的通项公式;
的通项公式;
(3)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日,小刘从各个渠道融资
日,小刘从各个渠道融资![]() 万元,在某大学投资一个咖啡店,
万元,在某大学投资一个咖啡店,![]() 年
年![]() 月
月![]() 日正式开业,已知开业第一年运营成本为
日正式开业,已知开业第一年运营成本为![]() 万元,由于工人工资不断增加及设备维修等,以后每年成本增加
万元,由于工人工资不断增加及设备维修等,以后每年成本增加![]() 万元,若每年的销售额为
万元,若每年的销售额为![]() 万元,用数列
万元,用数列![]() 表示前
表示前![]() 年的纯收入.(注:纯收入
年的纯收入.(注:纯收入![]() 前
前![]() 年的总收入
年的总收入![]() 前
前![]() 年的总支出
年的总支出![]() 投资额)
投资额)
(1)试求年平均利润最大时的年份(年份取正整数)并求出最大值.
(2)若前![]() 年的收入达到最大值时,小刘计划用前
年的收入达到最大值时,小刘计划用前![]() 年总收入的
年总收入的![]() 对咖啡店进行重新装修,请问:小刘最早从哪一年对咖啡店进行重新装修(年份取整数)?并求小刘计划装修的费用.
对咖啡店进行重新装修,请问:小刘最早从哪一年对咖啡店进行重新装修(年份取整数)?并求小刘计划装修的费用.
查看答案和解析>>
科目: 来源: 题型:
【题目】海关对同时从![]() 三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测.
三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测.
地区 |
|
|
|
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自![]() 各地区商品的数量;
各地区商品的数量;
(2)若在这6件样品中随机抽取2件送往甲机构进一步检测,求这2件商品来自相同地区的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,曲线C的参数方程是
轴的正半轴,建立平面直角坐标系,曲线C的参数方程是![]() ,(
,(![]() 为参数).
为参数).
(1)求直线![]() 被曲线C截得的弦长;
被曲线C截得的弦长;
(2)从极点作曲线C的弦,求各弦中点轨迹的极坐标方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明设计了一款正四棱锥形状的包装盒,如图所示,![]() 是边长为
是边长为![]() 的正方形硬纸片,切去阴影部分所示的四个全等的等腰三角形,再沿虚线折起,使得
的正方形硬纸片,切去阴影部分所示的四个全等的等腰三角形,再沿虚线折起,使得![]() 四个点重合于图中的点
四个点重合于图中的点![]() ,正好形成一个正四棱锥形状的包装盒,设正四棱锥底面正方形的边长为
,正好形成一个正四棱锥形状的包装盒,设正四棱锥底面正方形的边长为![]()
![]() .
.

(1)试用![]() 表示该四棱锥的高度
表示该四棱锥的高度![]() ,并指出
,并指出![]() 的取值范围;
的取值范围;
(2)若要求侧面积不小于![]() ,求该四棱锥的高度的最大值,并指出此时该包装盒的容积.
,求该四棱锥的高度的最大值,并指出此时该包装盒的容积.
查看答案和解析>>
科目: 来源: 题型:
【题目】2018年12月18日上午10时,在人民大会堂举行了庆祝改革开放40周年大会.40年众志成城,40年砥砺奋进,40年春风化雨,中国人民用双手书写了国家和民族发展的壮丽史诗.会后,央视媒体平台,收到了来自全国各地的纪念改革开放40年变化的老照片,并从众多照片中抽取了100张照片参加“改革开放40年图片展”,其作者年龄集中在![]() 之间,根据统计结果,做出频率分布直方图如下:
之间,根据统计结果,做出频率分布直方图如下:

(Ⅰ)求这100位作者年龄的样本平均数![]() 和样本方差
和样本方差![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(Ⅱ)由频率分布直方图可以认为,作者年龄X服从正态分布![]() ,其中
,其中![]() 近似为样本平
近似为样本平
均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)利用该正态分布,求![]() ;
;
(ii)央视媒体平台从年龄在![]() 和
和![]() 的作者中,按照分层抽样的方法,抽出了7人参加“纪念改革开放40年图片展”表彰大会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间
的作者中,按照分层抽样的方法,抽出了7人参加“纪念改革开放40年图片展”表彰大会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间![]() 的人数是Y,求变量Y的分布列和数学期望.附:
的人数是Y,求变量Y的分布列和数学期望.附:![]() ,若
,若![]() ,则
,则![]() ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别为
分别为![]() ,
,![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.
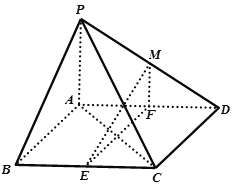
(1)若![]() 为
为![]() 的中点,求证:平面
的中点,求证:平面![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)若![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线关于![]() 轴对称,它的顶点在坐标原点,点
轴对称,它的顶点在坐标原点,点![]() 、
、![]() 、
、![]() 均在抛物线上.
均在抛物线上.
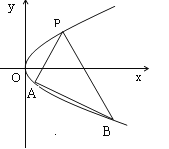
(1)写出该抛物线的方程及其准线方程;
(2)当![]() 与
与![]() 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求![]() 的值及直线
的值及直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知椭圆C:![]() 的左、右项点分别为A1,A2,左右焦点分别为F1,F2,离心率为
的左、右项点分别为A1,A2,左右焦点分别为F1,F2,离心率为![]() ,|F1F2|=
,|F1F2|=![]() ,O为坐标原点.
,O为坐标原点.
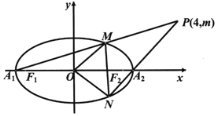
(1)求椭圆C的方程;
(2)设过点P(4,m)的直线PA1,PA2与椭圆分别交于点M,N,其中m>0,求![]() 的面积S的最大值.
的面积S的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,椭圆![]() 的离心率
的离心率![]() ,且椭圆C的短轴长为
,且椭圆C的短轴长为![]() .
.
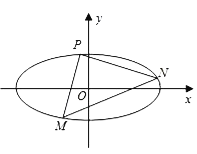
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 椭圆
椭圆![]() 上的三个动点.
上的三个动点.
(i)若直线![]() 过点D
过点D![]() ,且
,且![]() 点是椭圆
点是椭圆![]() 的上顶点,求
的上顶点,求![]() 面积的最大值;
面积的最大值;
(ii)试探究:是否存在![]() 是以
是以![]() 为中心的等边三角形,若存在,请给出证明;若不存在,请说明理由.
为中心的等边三角形,若存在,请给出证明;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com