【题目】已知函数，其中，为自然对数的底数.

（1）求函数的单调递增区间；

（2）当时，，求实数的取值范围.

【题目】某调研机构，对本地岁的人群随机抽取人进行了一次生活习惯是否符合低碳观念的调查，将生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，结果显示，有人为“低碳族”，该人的年龄情况对应的频率分布直方图如图.

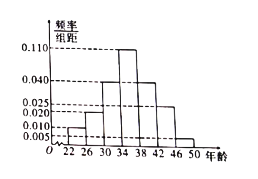
（1）根据频率分布直方图，估计这名“低碳族”年龄的平均值，中位数；

（2）若在“低碳族”且年龄在、的两组人群中，用分层抽样的方法抽取人，试估算每个年龄段应各抽取多少人？

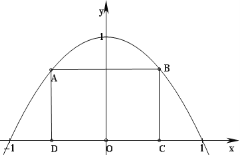
【题目】如图所示，抛物线与轴所围成的区域是一块等待开垦的土地，现计划在该区域内围出一块矩形地块ABCD作为工业用地，其中A、B在抛物线上，C、D在轴上.已知工业用地每单位面积价值为元，其它的三个边角地块每单位面积价值元.

（1）求等待开垦土地的面积；

（2）如何确定点C的位置，才能使得整块土地总价值最大.

【题目】已知椭圆的离心率，过点的直线与原点的距离为.

（1）求椭圆方程；

（2）若直线与椭圆交于两点，试求面积的范围.

（1）先完成上面的表格，并判断能否有90%的把握认为学生所学文理与阅读内容有关？

（2从300名被调查的学生中，随机进取30名学生，整理其日平均阅读时间（单位：分钟）如表：

试估计这30名学生日阅读时间的平均值（同一组中的数据以这组数据所在区间中点的值作代表）

（3）从（2）中日均阅读时间不低于120分钟的学生中随机选取2人介绍阅读心得，求这两人都是女生的概率.

参考公式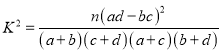： ，其中.

参考数据：

【题目】阿波罗尼斯（约公元前年）证明过这样一个命题:平面内到两定点距离之比为常数的点的轨迹是圆，后人将这个圆称为阿波罗尼斯圆.若平面内两定点、间的距离为，动点满足，则的最小值为（ ）

A. B. C. D.

【题目】抚州市某中学利用周末组织教职员工进行了一次秋季登军峰山健身的活动，有人参加，现将所有参加人员按年龄情况分为，，，，，，等七组，其频率分布直方图如下图所示．已知之间的参加者有4人．

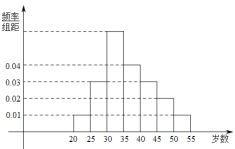
（1）求和之间的参加者人数；

（2）组织者从之间的参加者（其中共有名女教师包括甲女，其余全为男教师）中随机选取名担任后勤保障工作，求在甲女必须入选的条件下，选出的女教师的人数为2人的概率.

（3）已知和之间各有名数学教师，现从这两个组中各选取人担任接待工作，设两组的选择互不影响，求两组选出的人中都至少有名数学教师的概率?

【题目】在三棱锥中，，若平面平面，则三棱锥外接球的表面积为_______．

【题目】设分别是椭圈的左、右焦点，是椭圆上第二象限内的一点且与轴垂直，直线与椭圆的另一个交点为.

（1）若直线的斜率为，求椭圆的离心率；

（2）若直线与轴的交点为，且求.

【题目】凤鸣山中学的高中女生体重 (单位：kg)与身高(单位：cm)具有线性相关关系，根据一组样本数据（），用最小二乘法近似得到回归直线方程为，则下列结论中不正确的是（ ）

A.与具有正线性相关关系

B.回归直线过样本的中心点

C.若该中学某高中女生身高增加1cm，则其体重约增加0.85kg

D.若该中学某高中女生身高为160cm，则可断定其体重必为50.29kg.