若该学生数学竞赛获省一等奖，则该学生估计进入国家集训队的概率是0.2.若进入国家集训队，则提前录取，若未被录取，则再按②、③顺序依次录取：前面已经被录取后，不得参加后面的考试或录取.（注：自主招生考试通过且高考达重点线才能录取）

（Ⅰ）求该学生参加自主招生考试的概率；

（Ⅱ）求该学生参加考试的次数的分布列及数学期望；

（Ⅲ）求该学生被该校录取的概率.

A.40.6，1.1B.48.8，4.4C.81.2，44.4D.78.8，75.6

【题目】已知函数有两个极值点.

（Ⅰ）求的取值范围；

（Ⅱ）设，是的两个极值点，证明：.

【题目】已知抛物线的准线为，为上一动点，过点作抛物线的切线，切点分别为.

（I）求证：是直角三角形；

（II）轴上是否存在一定点，使三点共线.

【题目】如图，在四棱锥中，底面是平行四边形，平面，，，，为的中点.

（Ⅰ）求证：平面；

（Ⅱ）若，求二面角的大小.

A.7B.5C.4D.3

A. 甲的极差是29 B. 甲的中位数是24

C. 甲罚球命中率比乙高 D. 乙的众数是21

【题目】已知抛物线上横坐标为的点到焦点的距离为.

（1）求抛物线的方程；

（2）若过点的直线与抛物线交于不同的两点，且以为直径的圆过坐标原点，求的面积。

【题目】如图，三棱柱中，平面，，,点在线段上，且,.

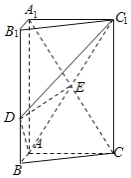
（1）试用空间向量证明直线与平面不平行；

（2）设平面与平面所成的锐二面角为，若，求的长；

（3）在（2）的条件下，设平面平面，求直线与平面的所成角.

【题目】已知函数，为实数）有极值，且在处的切线与直线平行.

（1）求实数的取值范围；

（2）是否存在实数，使得函数的极小值为1，若存在，求出实数的值；若不存在，请说明理由；

（3）设函数 试证明：在上恒成立并证明