
科目: 来源: 题型:
【题目】过函数![]() 的图象
的图象![]() 上一点
上一点![]() 作倾斜角互补的两条直线,分别与
作倾斜角互补的两条直线,分别与![]() 交与异于
交与异于![]() 的
的![]() ,
,![]() 两点.
两点.
(1)求证:直线![]() 的斜率为定值;
的斜率为定值;
(2)如果![]() ,
,![]() 两点的横坐标均不大于0,求
两点的横坐标均不大于0,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题满分14分)已知过原点的动直线![]() 与圆
与圆![]()
![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .
.
(1)求圆![]() 的圆心坐标;
的圆心坐标;
(2)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)是否存在实数![]() ,使得直线
,使得直线![]()
![]() 与曲线
与曲线![]() 只有一个交点?若存在,求出
只有一个交点?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】设椭圆![]()
![]() 的一个焦点为
的一个焦点为![]() ,且椭圆
,且椭圆![]() 过点
过点![]() ,
,![]() 为坐标原点,
为坐标原点,
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆![]() 恒有两个交点
恒有两个交点![]() 、
、![]() ,且
,且![]() ?若存在,写出该圆的方程,并求
?若存在,写出该圆的方程,并求![]() 的最大值,若不存在说明理由.
的最大值,若不存在说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题满分12分)
已知![]() =12sin(x+
=12sin(x+![]() )cosx-3,x∈[o,
)cosx-3,x∈[o,![]() ].
].
(1)求![]() 的最大值、最小值;
的最大值、最小值;
(Ⅱ)CD为△ABC的内角平分线,已知AC=![]() max,BC=
max,BC=![]() ,CD=2
,CD=2![]() ,求∠C.
,求∠C.
查看答案和解析>>
科目: 来源: 题型:
【题目】在“新零售”模式的背景下,某大型零售公司推广线下分店,计划在S市的A区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格.记x表示在各区开设分店的个数,y表示这个x个分店的年收入之和.

(1)该公司已经过初步判断,可用线性回归模型拟合y与x的关系,求y关于x的线性回归方程![]()
(2)假设该公司在A区获得的总年利润z(单位:百万元)与x,y之间的关系为![]() ,请结合(1)中的线性回归方程,估算该公司应在A区开设多少个分店时,才能使A区平均每个分店的年利润最大?
,请结合(1)中的线性回归方程,估算该公司应在A区开设多少个分店时,才能使A区平均每个分店的年利润最大?
(参考公式:![]() ,其中
,其中 ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知极坐标系的极点为直角坐标系xOy的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,圆C的直角坐标方程为![]() ,直线l的参数方程为
,直线l的参数方程为![]() (t为参数),射线OM的极坐标方程为
(t为参数),射线OM的极坐标方程为![]() .
.
(1)求圆C和直线l的极坐标方程;
(2)已知射线OM与圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】启东市政府拟在蝶湖建一个旅游观光项目,设计方案如下:如图所示的圆O是圆形湖的边界,沿线段AB,BC,CD,DA建一个观景长廊,其中A,B,C,D是观景长廊的四个出入口且都在圆O上,已知:BC=12百米,AB=8百米,在湖中P处和湖边D处各建一个观景亭,且它们关于直线AC对称,在湖面建一条观景桥APC.观景亭的大小、观景长廊、观景桥的宽度均忽略不计,设![]() .
.
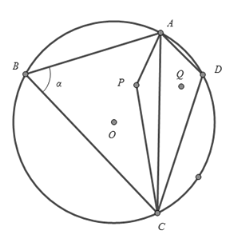
(1)若观景长廊AD=4百米,CD=AB,求由观景长廊所围成的四边形ABCD内的湖面面积;
(2)当![]() 时,求三角形区域ADC内的湖面面积的最大值;
时,求三角形区域ADC内的湖面面积的最大值;
(3)若CD=8百米且规划建亭点P在三角形ABC区域内(不包括边界),试判断四边形ABCP内湖面面积是否有最大值?若有,求出最大值,并写出此时![]() 的值;若没有,请说明理由.
的值;若没有,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校100名学生的数学测试成绩的频率分布直方图如图所示,分数不低于a即为优秀,如果优秀的人数为20,则a的估计值是( )
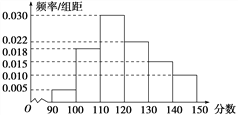
A. 130 B. 140 C. 133 D. 137
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com