
科目: 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,直线
,直线![]() 与椭圆C交于A,B两点,且
与椭圆C交于A,B两点,且![]() .
.
(1)求椭圆C的方程.
(2)不经过点![]() 的直线
的直线![]() 被圆
被圆![]() 截得的弦长与椭圆C的长轴长相等,且直线
截得的弦长与椭圆C的长轴长相等,且直线![]() 与椭圆C交于D,E两点,试判断
与椭圆C交于D,E两点,试判断![]() 的周长是否为定值?若是,求出定值;若不是,请说明理由.
的周长是否为定值?若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于函数![]() ,若
,若![]() 满足
满足![]() ,则称
,则称![]() 为函数
为函数![]() 的一阶不动点,若
的一阶不动点,若![]() 满足
满足![]() ,则称
,则称![]() 为函数
为函数![]() 的二阶不动点,若
的二阶不动点,若![]() 满足
满足![]() ,且
,且![]() ,则称
,则称![]() 为函数
为函数![]() 的二阶周期点.
的二阶周期点.
(1)设![]() .
.
①当![]() 时,求函数
时,求函数![]() 的二阶不动点,并判断它是否是函数数
的二阶不动点,并判断它是否是函数数![]() 的二阶周期点;
的二阶周期点;
②已知函数![]() 存在二阶周期点,求k的值;
存在二阶周期点,求k的值;
(2)若对任意实数b,函数![]() 都存在二阶周期点,求实数c的取值范围.
都存在二阶周期点,求实数c的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某科技公司新研制生产一种特殊疫苗,为确保疫苗质量,定期进行质量检验.某次检验中,从产品中随机抽取100件作为样本,测量产品质量体系中某项指标值,根据测量结果得到如下频率分布直方图:

(1)求频率分布直方图中![]() 的值;
的值;
(2)技术分析人员认为,本次测量的该产品的质量指标值X服从正态分布![]() ,若同组中的每个数据用该组区间的中间值代替,计算
,若同组中的每个数据用该组区间的中间值代替,计算![]() ,并计算测量数据落在(187.8,212.2)内的概率;
,并计算测量数据落在(187.8,212.2)内的概率;
(3)设生产成本为y元,质量指标值为![]() ,生产成本与质量指标值之间满足函数关系
,生产成本与质量指标值之间满足函数关系![]() 假设同组中的每个数据用该组区间的中间值代替,试计算生产该疫苗的平均成本.
假设同组中的每个数据用该组区间的中间值代替,试计算生产该疫苗的平均成本.
参考数据:![]() ,
,![]()
![]()
![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() ,
,![]() )图象上两个相邻的最值点为
)图象上两个相邻的最值点为![]() 和
和![]()
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 在区间
在区间![]() 上的对称中心、对称轴;
上的对称中心、对称轴;
(3)将函数![]() 图象上每一个点向右平移
图象上每一个点向右平移![]() 个单位得到函数
个单位得到函数![]() ,令
,令![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最大值,并指出此时x的值.
上的最大值,并指出此时x的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知某个机械零件是由两个有公共底面的圆锥组成的,且这两个圆锥有公共点的母线互相垂直,把这个机械零件打磨成球形,该球的半径最大为1,设这两个圆锥的高分别为![]() ,则
,则![]() 的最小值为__________.
的最小值为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】国家的精准扶贫极大地激发了农村贫困村民的生产积极性.新春伊始,某村计划利用2019年国家专项扶贫款120万元兴建两个扶贫产业:毛驴养殖和蔬菜温室大棚.建一个养殖场的费用是9万元,建一个温室大棚的费用是12万元.根据村民意愿,养殖场至少要建3个,温室大棚至少要建2个,并且由于建设用地的限制,养殖场的数量不能超过温室大棚数量的2倍,则建养殖场和温室大棚个数之和的最大值为__________.
查看答案和解析>>
科目: 来源: 题型:
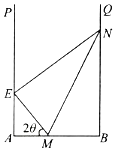
【题目】某地拟在一个U形水面PABQ(∠A=∠B=90°)上修一条堤坝(E在AP上,N在BQ上),围出一个封闭区域EABN,用以种植水生植物.为了美观起见,决定从AB上点M处分别向点E,N拉2条分隔线ME,MN,将所围区域分成3个部分(如图),每部分种植不同的水生植物.已知AB=a,EM=BM,∠MEN=90°,设所拉分隔线总长度为l.
(1)设∠AME=2θ,求用θ表示的l函数表达式,并写出定义域;
(2)求l的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com