
科目: 来源: 题型:
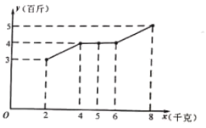
【题目】某基地蔬菜大棚采用水培、无土栽培方式种植各类菠菜.根据统计,该基地的西红种增加量y(百斤)与使用某种液体肥料x(千克)之间对应数据为如图所示的折线图.依据折线图及其提供的数据,是否可用线性回归模型拟合y与x的关系?如果可以,请计算相关系数r并加以说明(精确到0.01),(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
附:相关系数公式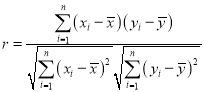 ,参考数据:
,参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地级市共有![]() 中小学生,其中有
中小学生,其中有![]() 学生在
学生在![]() 年享受了“国家精准扶贫”政策,在享受“国家精准扶贫”政策的学生中困难程度分为三个等次:一般困难、很困难、特别困难,且人数之比为
年享受了“国家精准扶贫”政策,在享受“国家精准扶贫”政策的学生中困难程度分为三个等次:一般困难、很困难、特别困难,且人数之比为![]() ,为进一步帮助这些学生,当地市政府设立“专项教育基金”,对这三个等次的困难学生每年每人分别补助
,为进一步帮助这些学生,当地市政府设立“专项教育基金”,对这三个等次的困难学生每年每人分别补助![]() 元、
元、![]() 元、
元、![]() 元,经济学家调查发现,当地人均可支配年收入较上一年每增加
元,经济学家调查发现,当地人均可支配年收入较上一年每增加![]() ,一般困难的学生中有
,一般困难的学生中有![]() 会脱贫,脱贫后将不再享受“精准扶贫”政策,很困难的学生中有
会脱贫,脱贫后将不再享受“精准扶贫”政策,很困难的学生中有![]() 转为一般困难,特别困难的学生中有
转为一般困难,特别困难的学生中有![]() 转为很困难.现统计了该地级市
转为很困难.现统计了该地级市![]() 年到
年到![]() 年共
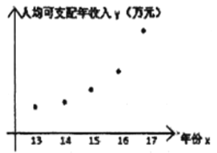
年共![]() 年的人均可支配年收入,对数据初步处理后得到了如图所示的散点图和表中统计量的值,其中年份
年的人均可支配年收入,对数据初步处理后得到了如图所示的散点图和表中统计量的值,其中年份![]() 取
取![]() 时代表
时代表![]() 年,
年,![]() 与
与![]() (万元)近似满足关系式
(万元)近似满足关系式![]() ,其中
,其中![]() ,
,![]() 为常数.(
为常数.(![]() 年至
年至![]() 年该市中学生人数大致保持不变)
年该市中学生人数大致保持不变)
|
|
|
|
|
|
|
|
|
|
|
|
其中![]() ,
,![]()
(1)估计该市![]() 年人均可支配年收入;
年人均可支配年收入;
(2)求该市![]() 年的“专项教育基金”的财政预算大约为多少?
年的“专项教育基金”的财政预算大约为多少?
附:对于一组具有线性相关关系的数据![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线方程
,其回归直线方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为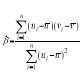 ,
,![]()
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目: 来源: 题型:
【题目】若函数y=f(x)(x∈R)满足f(1+x)=f(1-x)且x∈[-1,1]时,f(x)=1-x2,函数g(x)=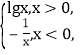 则函数h(x)=f(x)-g(x)在区间[-5,5]内的零点的个数为
则函数h(x)=f(x)-g(x)在区间[-5,5]内的零点的个数为
A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,在点
,在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)已知![]() ,当
,当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)对于在![]() 中的任意一个常数
中的任意一个常数![]() ,是否存在正数
,是否存在正数![]() ,使得
,使得![]() ,请说明理由。
,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】中国海军,正在以不可阻挡的气魄向深蓝进军。在中国海军加快建设的大背景下,国产水面舰艇吨位不断增大、技术日益现代化,特别是国产航空母舰下水,航母需要大量高素质航母舰载机飞行员。为此中国海军在全国9省9所优质普通高中进行海航班建设试点培育航母舰载机飞行员。2017年4月我省首届海军航空实验班开始面向全省遴选学员,有10000名初中毕业生踊跃报名投身国防,经过文化考试、体格测试、政治考核、心理选拔等过程筛选,最终招收50名学员。培养学校在关注学员的文化素养同时注重学员的身体素质,要求每月至少参加一次野营拉练活动(下面简称“活动”)并记录成绩.10月某次活动中海航班学员成绩统计如图所示:
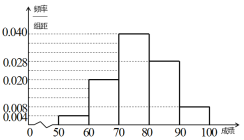
(Ⅰ)根据图表,试估算学员在活动中取得成绩的中位数(精确到![]() );
);
(Ⅱ)根据成绩从![]() 、
、![]() 两组学员中任意选出两人为一组,若选出成绩分差大于
两组学员中任意选出两人为一组,若选出成绩分差大于![]() ,则称该组为“帮扶组”,试求选出两人为“帮扶组”的概率.
,则称该组为“帮扶组”,试求选出两人为“帮扶组”的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】十九世纪末:法国学者贝特朗在研究几何概型时提出了“贝特朗悖论”,即“在一个圆内任意选一条弦,这条弦的弦长长于这个圆的内接等边三角形边长的概率是多少?”贝特朗用“随机半径”“随机端点”“随机中点”三个合理的求解方法,但结果都不相同.该悖论的矛头直击概率概念本身,强烈地刺激了概率论基础的严格化.已知“随机端点”的方法如下:设![]() 为圆
为圆![]() 上一个定点,在圆周上随机取一点
上一个定点,在圆周上随机取一点![]() ,连接
,连接![]() ,所得弦长
,所得弦长![]() 大于圆
大于圆![]() 的内接等边三角形边长的概率.则由“随机端点”求法所求得的概率为( )
的内接等边三角形边长的概率.则由“随机端点”求法所求得的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知a∈R,函数f(x)=(-x2+ax)ex(x∈R).
(1)当a=2时,求函数f(x)的单调区间;
(2)若函数f(x)在(-1,1)上单调递增,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 与抛物线
与抛物线![]() 的一个公共点,且椭圆与抛物线具有一个相同的焦点
的一个公共点,且椭圆与抛物线具有一个相同的焦点![]() .
.
(1)求椭圆![]() 及抛物线
及抛物线![]() 的方程;
的方程;
(2)设过![]() 且互相垂直的两动直线
且互相垂直的两动直线![]() ,
,![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的最小值
面积的最小值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com